CS3240: Data Structures and Algorithms

Regarding the efficiency of algorithms, the rapid advances in computer technology make physical measures (run-time, memory requirements) less relevant. A more standardized measure is the number of elementary computer operations it takes to solve the problem in the worst case. Average performance is not safe. There may be particular cases (technically called instances of a problem) that behave much worse than the average and nobody can afford to rely on his/her luck.

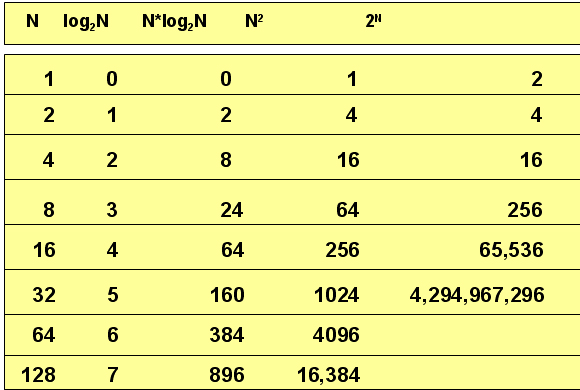
The number of elementary operations depends of course on the "size" of the problem data. Sorting 1 billion numbers is quite different from sorting 10 ones, so we express the number of elementary operations (expected in the worst-case scenario) as a function of some characteristic number(s) that suffice to capture the volume of the work to be done. For a sorting algorithm, this number is simply the number n of numbers to be sorted.

Now, suppose an algorithm solves a problem of size n in at most 7n^³ + 5n^² + 27 operations.

For such functions, we are primarily interested in their rate of growth as n increases. We want to distinguish between mild and "exploding" growth rates, therefore differences as that between 7n^{^3} and n^{^3} are not really important (besides, large differences in the constants do not arise in practice). We can also discard the lower order terms, because at large sizes it is the highest degree that determines the rate of growth.

The end result is that the complexity of this algorithm can be sufficiently described by the function g(n) = n^³. Formally, we say that this algorithm is "of order O(n^³)". It is also usual to say that this algorithm "takes time O(n^{^3})". This symbolism is a reminder that this function expresses the worst-case behavior at sufficiently large sizes.

Note that for sufficiently large n:
logn < n < nlogn < n^{^2} < n^³ < 2^{^n}

This is sometimes stated as:
O(logn) < O(n ) < O(nlogn) < O(n^²) < O(n^³) < O(2^ⁿ)

Counting Time

Worst Versus Average Case

The order of magnitude, or Big-O notation,

expresses the computing time of a problem as the term in a function that increases most rapidly relative to the size of a problem.

 

O(1)	bounded (by a constant) time
O(log2N)	logarithmic time
O(N)	linear time
O(N*logN)	N*log2N time
O(N^2)	quadratic time
O( 2^N )	exponential time

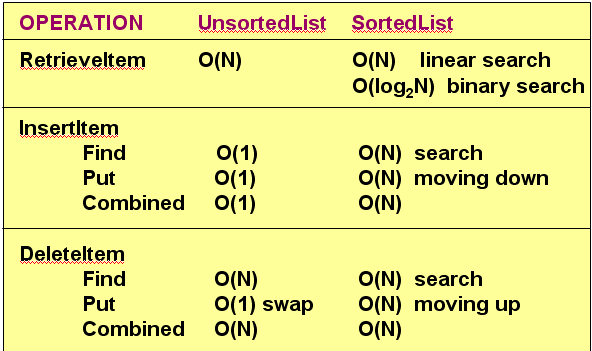
List Operations Complexity