CS3240: Data Structures and Algorithms

1. Uniformed Cost Measure: The idea behind this method is that each operation takes a constant amount of time. The advantage of this method is simplicity. In most cases, it gives a good estimation of the running time, but there are some instances where this method is overly simple. For example, adding two 100,000 digit numbers will take more time than adding two single digit numbers. Saying they both take the same constant time is misleading.

2. Logarithmic Cost Measure: This method offers a better estimation in the example mentioned above. Its main premise is that the time of an algorithm will always be proportional to lg n where n is the input size. Using the above example, adding two numbers will be O(lg n) instead of O(1). The reasoning behind this stems from the fact that adding two integers of size n will take time proportional to the number of bits in the integers. This will require at most lg n bits to store in memory. For example, suppose we have a value n. In binary,
   

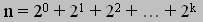
   where k is the largest power of two in the representation of n. It follows that

   

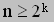
   Taking the log of both sides, we get

   

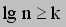
   In other words, the representation of n in memory is at most lg n bits. If the time taken to add two numbers is dependent on their size (ie. the space the values take up in memory), the time will be proportional to lg n. This method is more realistic, but it tends to be impractical since it requires more sophisticated computations.

3. A Compromise: This method is a combination of the two above methods. If an operation involves values less than or equal to n^c where c is some large finite constant, that operation is considered to take constant time. Operations where the values are greater than n^c take times that are proportional to lg n. The reason for this is similar to before:
   

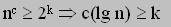
Remark: "lg n" is equivalent to "log base 2 of n".