|
||||||
|
Segmentation: Region-based
- Edge-based segmentation: borders between regions
- Region-based segmentation: direct construction of regions
- It is easy to construct regions from their borders and it is easy to detect borders of existing regions.
- Segmentations resulting from edge-based methods and region growing methods are not usually exactly the same.
- Combination of results may often be a good idea.
- Region growing techniques are generally better in noisy images where edges are extremely difficult to detect.
- Homogeneity of regions is used as the main segmentation criterion in
region growing.
- The criteria for homogeneity:
- gray level
- color, texture
- shape
- model
- The criteria for homogeneity:
- Regions have already been defined
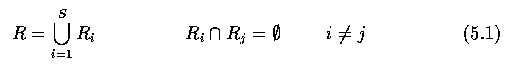
- Further assumptions:
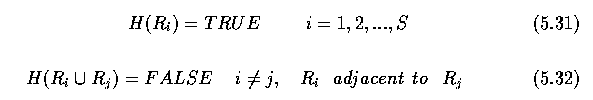
- Resulting regions of the segmented image must be both homogeneous and maximal.
Region merging

- Specific methods differ in the definition of the starting segmentation and in the criterion for merging.
- The result of region merging usually depends on the order in which regions are merged.
- The simplest methods begin merging by starting the segmentation using regions of 2x2, 4x4 or 8x8 pixels.
- Region descriptions are then based on their statistical gray level properties.
- A region description is compared with the description of an adjacent region; if they match, they are merged into a larger region and a new region description is computed. Otherwise regions are marked as non-matching.
- Merging of adjacent regions continues between all neighbors, including newly formed ones. If a region cannot be merged with any of its neighbors, it is marked `final' and the merging process stops when all image regions are so marked.

- The data structure called supergrid carries all the necessary information for region merging in 4-adjacency using crack edges.
- Merging heuristics:
- Two adjacent regions are merged if a significant part of their common boundary consists of weak edges
- Two adjacent regions are also merged if a significant part of their common boundary consists of weak edges, but in this case not considering the total length of the region borders.
- Of the two given heuristics, the first is more general and the second
cannot be used alone because it does not consider the influence of different
region sizes.
- Edge significance can be evaluated according to the formula
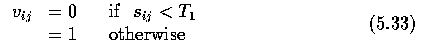
where v_ij=1 indicates a significant edge, v_ij=0 a weak edge, T_1 is a preset threshold, and s_ij is the crack edge value.

- The supergrid data structure allows precise work with edges and borders but a big disadvantage of this data structure is that it is not suitable for the representation of regions.
- A good data structure to use can be a planar region adjacency graph.

- Region splitting is the opposite of region merging.
- It begins with the whole image represented as a single region which does not usually satisfy the condition of homogeneity.
- The existing image regions are sequentially split to satisfy all the above given conditions of homogeneity.
- Region splitting does not result in the same segmentation even if the same
homogeneity criteria are used.
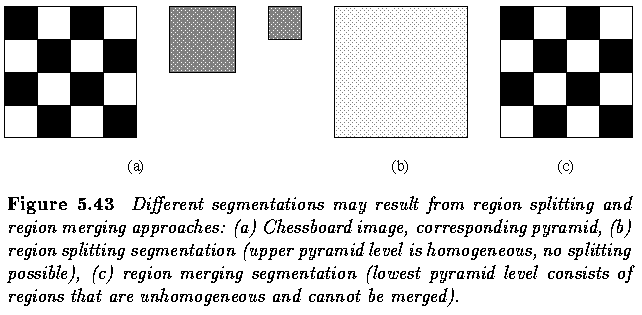
- Region splitting methods generally use similar criteria of homogeneity as region merging methods, and only differ in the direction of their application.
- A combination of splitting and merging may result in a method with the advantages of both approaches.
- Split-and-merge approaches work using pyramid image representations;
regions are square-shaped and correspond to elements of the appropriate
pyramid level.
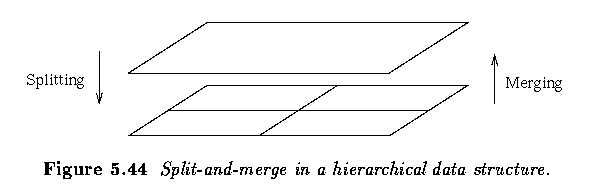
- If any region in any pyramid level is not homogeneous (excluding the lowest level), it is split into four subregions -- these are elements of higher resolution at the level below.
- If four regions exist at any pyramid level with approximately the same value of homogeneity measure, they are merged into a single region in an upper pyramid level.
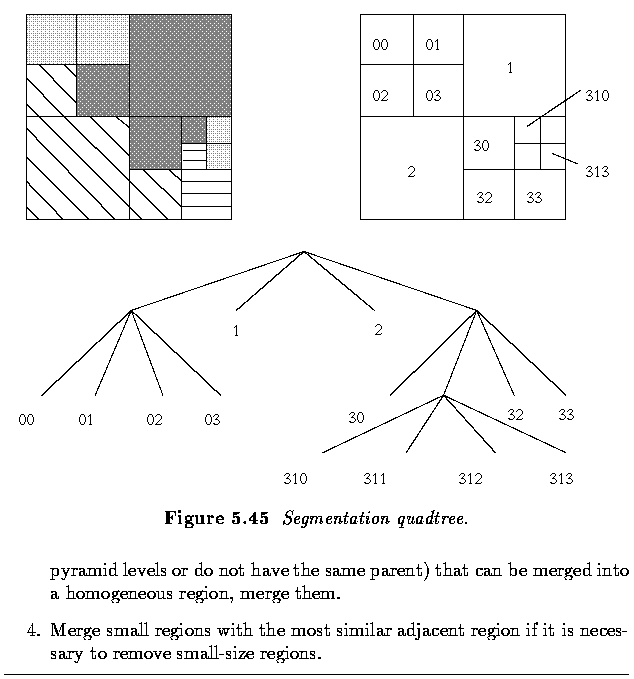
- The segmentation process can be understood as the construction of a segmentation quadtree where each leaf node represents a homogeneous region.
- Splitting and merging corresponds to removing or building parts of the segmentation quadtree.
- Split-and-merge methods usually store the adjacency information in region adjacency graphs (or similar data structures).
- Using segmentation trees, in which regions do not have to be contiguous, is both implementationally and computationally easier.
- An unpleasant drawback of segmentation quadtrees is the square region
shape assumption
- merging of regions which are not part of the same branch of the segmentation tree
- Because both split-and-merge processing options are available, the starting segmentation does not have to satisfy any of the homogeneity conditions.

- A pyramid data structure with overlapping regions is an interesting modification of this method.
- Each region has four potential parent elements in the upper pyramid level and sixteen possible child elements in the lower pyramid level.
- Segmentation tree generation begins in the lowest pyramid level. Properties of each region are compared with properties of each of its potential parents and the segmentation branch is linked to the most similar of them.
- After construction of the tree is complete, all the homogeneity values of all the elements in the pyramid data structure are recomputed to be based on child-region properties only.
- This recomputed pyramid data structure is used to generate a new segmentation tree, beginning again at the lowest level.
- The pyramid updating process and new segmentation tree generation is repeated until no significant segmentation changes can be detected between steps.
- The highest level of the segmentation tree must correspond to the expected number of image regions and the pyramid height defines the maximum number of segmentation branches.
- If the number of regions in an image is less than 2^n, some regions can be represented by more than one element in the highest pyramid level.

- Considerably lower memory requirements can be found in a single-pass split-and-merge segmentation.
- A local splitting pattern is detected in each 2x2 pixel image block and
regions are merged in overlapping blocks of the same size.

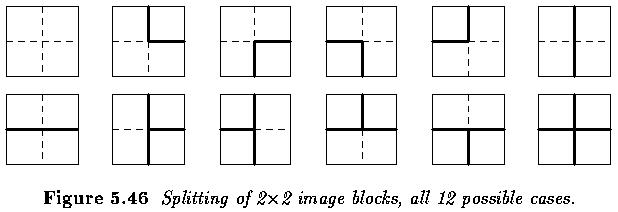
- The image blocks overlap during the image search.
- Except for locations at the image borders, three of the four pixels have been assigned a label in previous search locations, but these labels do not necessarily match the splitting pattern found in the processed block.
- If a mismatch is detected in step 3 of the algorithm, it is necessary to resolve possibilities of merging regions that were considered separate so far - to assign the same label to two regions previously labeled differently.
- Two regions R_1 and R_2 are merged into a region R_3 if
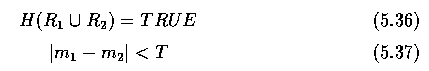
- where m_1 and m_2 are the mean gray level values in regions R_1 and R_2, and T is some appropriate threshold.
- If region merging is not allowed, regions keep their previous labels.
- If larger blocks are used, more complex image properties can be included in the homogeneity criteria (even if these larger blocks are divided into 2x2 sub-blocks to determine the splitting pattern).
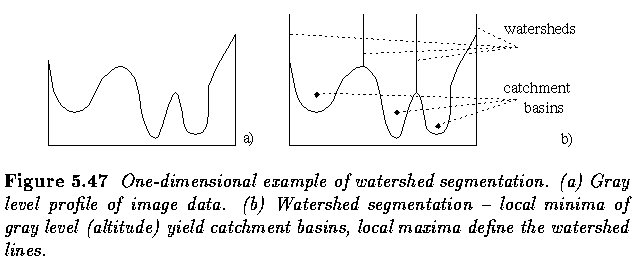
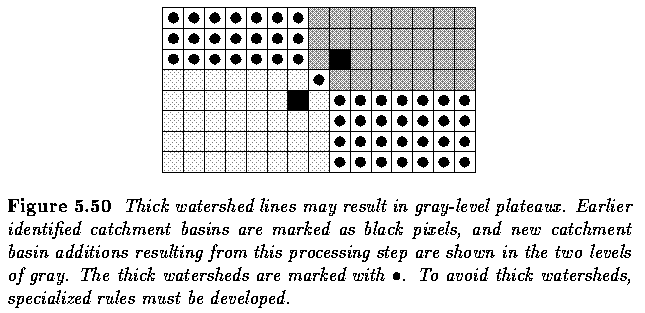
Watersheds

Region growing post-processing
- Region growing often results in undergrowing or overgrowing as a result of non-optimal parameter setting.
- A variety of post-processors has been developed.
- Some of them combine segmentation information obtained from region growing and edge-based segmentation.
- Simpler post-processors are based on general heuristics and decrease the number of small regions in the segmented image that cannot be merged with any adjacent region according to the originally applied homogeneity criteria.

- This algorithm will execute much faster if all regions smaller than a preselected size are merged with their neighbors without having to order them by size.
