Neural Network
What is Neural Network?
A neural network is an artificial representation of
the human brain that tries to simulate its learning process. Like the
human brain, a neural net also consists of neurons and connections between
them. The neurons are transporting incoming information on their outgoing
connections to other neurons. In neural net terms these connections
are called weights. The "electrical" information is simulated
with specific values stored in those weights. By simply changing these
weight values the changing of the connection structure can also be simulated.
The following figure shows an idealized neuron of a neural net.
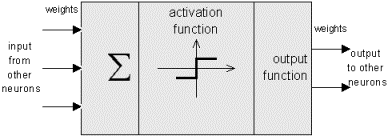Figure N-1
As you can see, an artificial neuron looks similar to a biological neural cell. And it works in the same way. Information (called the input) is sent to the neuron on its incoming weights. This input is processed by a propagation function that adds up the values of all incoming weights. The resulting value is compared with a certain threshold value by the neuron's activation function. If the input exceeds the threshold value, the neuron will be activated, otherwise it will be inhibited. If activated, the neuron sends an output on its outgoing weights to all connected neurons and so on.
In a neural
net, the neurons are grouped in layers, called neuron layers. Usually
each neuron of one layer is connected to all neurons of the preceding
and the following layer (except the input layer and the output layer
of the net). The information given to a neural net is propagated layer-by-layer
from input layer to output layer through either none, one or more hidden
layers. Depending on the learning algorithm, it is also possible that
information is propagated backwards through the net. The Figure N-2
shows a neural net with three neuron layers.
Backpropagation Neural Network
The
Backpropagation Net was first introduced by G.E. Hinton, E. Rumelhart
and R.J. Williams in 1986 and is one of the most powerful neural net
types. It has the same structure as the Multi-Layer-Perceptron and uses
the backpropagation learning algorithm. Figure N-3 shows backpropagation
net diagram.
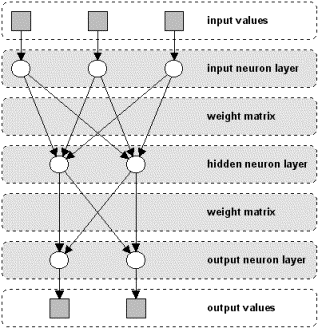
Figure N-2
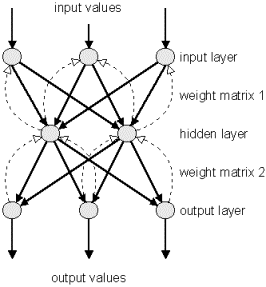
Figure N-3
Backpropagation
Net is a Feed-Forward, supervised neural network that uses backpropagarion
algorithm for learning.
Learning Methods
As
mentioned before, neural nets try to simulate the human brain's ability
to learn. That is, the artificial neural net is also made of neurons
and dendrites. Unlike the biological model, a neural net has an unchangeable
structure, built of a specified number of neurons and a specified number
of connections between them (called "weights"), which have
certain values. What changes during the learning process are the values
of those weights. Compared to the original this means: Incoming information
"stimulates" (exceeds a specified threshold value of) certain
neurons that pass the information to connected neurons or prevent further
transportation along the weighted connections. The value of a weight
will be increased if information should be transported and decreased
if not.
While
learning different inputs, the weight values are changed dynamically
Backpropagation Algorithm
Backpropagation
is a supervised learning algorithm and is mainly used by Multi-Layer-Perceptrons
to change the weights connected to the net's hidden neuron layer(s).
The backpropagation algorithm uses a computed output error to
change the weight values in backward direction. To get this net error,
a forwardpropagation phase must have been done before. While propagating
in forward direction, the neurons are being activated using the sigmoid
activation function.
The
formula of sigmoid activation is:
f(x)
= 1 / 1 + e ^ -input
The
algorithm works as follows:
1.
Perform the forwardpropagation phase for an input pattern and calculate
the output error.
2.
Change all weight values of each weight matrix using the formula
weight(old) + learning rate * output error * output(neurons(neurons
i) * output(neurons i+1) * ( 1 - output(neurons i+1) )
3.
Go to step 1
4.
The algorithm ends, if all output patterns match their target patterns
Training Neural Network
NN is trained with {Feature Vector, Class Identification} pairs. Figure 7 shows the example of our neural network
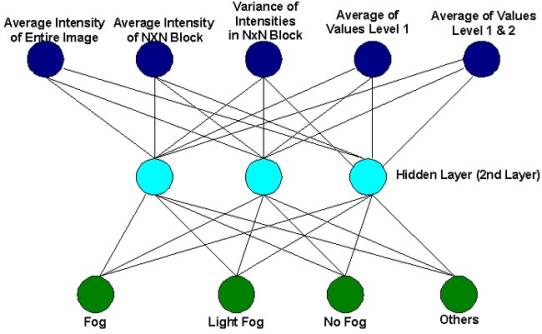
Figure 7
NN Options and
Training Options:
· Layer
2 Size
A
type of neuron Layer that lies between a neural net's input and output
layers. Its neuron values are not visible outside the net. The usage
of this layers extends a neural net's ability to learn logical operations.
Default:
5
·Learning
Rate
A
changeable value used by the learning algorithms, which effects the
changing of weight values. The greater the learning rate, the
more
the weight values are changed. Is usually decreased during the learning
process.
Default:
0.5
· Global
Error
Used
by neural nets with supervised learning, by comparing the current output
values with the desired output values of the net. The smaller the net's
error is, the better the net had been trained. Usually the error is
always a value greater than zero.
Default:
0.9
· Maximum
Iterations
Maximum Iterations determines how many times neural network repeat its learning process if the desired global error value is not achieved.
Default:
10000
Java Package for NN -
JaNet
jaNet was created by two students, Wilfred Gander and Lorenzo Patocchi at Biel School of Engineering.
jaNet
package is a Java neural network toolkit. With jaNet one can design,
test, train and optimize an ideal neural network for private applications. When the network is ready, one can save it
in a file and then include such network in private applications using
the jaNet.backprop package.
The
package can be found at their home page. http://zwww.isbiel.ch/I/Projects/janet/index.html