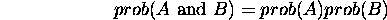|
||||||
|
Probability
Probability is about the odds that a given event (or set of events) will occur. The weatherperson might say that the probability of rain this afternoon is 10%, meaning that, in the long run, 10% of the days on which such a prediction is made will have some rain, and the other 90% will have no rain.Any discussion of probability requires considering the set of possible outcomes or states or situations. We assume that exactly one state from a set occurs at any time. If there is a set of a fixed size, then the calculations are much easier, however, sometimes, the set is of infinite size such as the set of all possible temperatures between 0 and 100 degrees.
If the set 
is finite
then there is a probability 
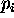that each member 
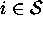can occur, such that:
since one state must be true at any time. If the set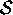 
is infinite, then the probability of
any specific state is zero; rather, we assign discrete probabilities to ranges
of values from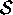 
. Assuming
that the values in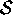 
are
continuous, then the usual notion of probability is the probability that the
variable x is between two values:
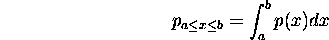
where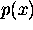 
is the
probability density that describes the distribution of the likelihood
that a given event or value of x occurs. As with discrete probabilities,
some event must occur so:
The Cummulative Distrubution Function P(a), in the
discrete case is the sum of the density function, 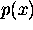from 0 to
a. In the continous case, the sum is replaced by an integral.
One common continuous distribution is the uniform distribution, which has all possible values being equally likely between the upper and lower bound of the possible values. If the range of possible values is from a to b, then the probability density is:
Another common continuous distribution is the gaussian or normal
distribution, which can have any possible value, but whose values are
clustered about a mean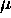 
,
and the degree to which they are clustered is determined by the standard
deviation parameter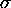 
:
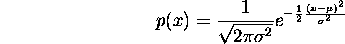
One often talks about events or measurements being independent. This means that the variations in the value of the first has no relation to the variations in the value of the second event or measurement. This allows us to calculate the probability of a pair of events A and B as:
