CS6825: Computer Vision |
||||||
|
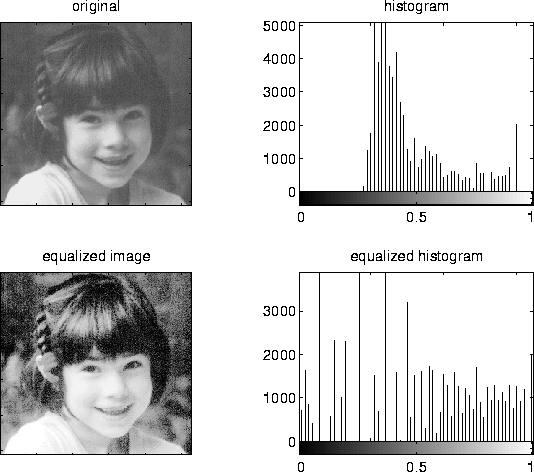
Histogram Equalization
| Original | Histogram Equalized |
Histogram equalization is a common technique for enhancing the appearance of images. Suppose we have an image which is predominantly dark. Then its histogram would be skewed towards the lower end of the grey scale and all the image detail is compressed into the dark end of the histogram. If we could `stretch out' the grey levels at the dark end to produce a more uniformly distributed histogram then the image would become much clearer.
 |
How do we determine this grey scale transformation function? Assume our grey levels are continuous and have been normalized to lie between 0 and 1.
We must find a transformation T that maps grey values r in the
input image F to grey values s = T(r) in the
transformed image ![]() .
.
It is assumed that
- T is single valued and monotonically increasing, and
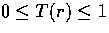 for
for 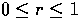 .
.
r = T-1(s).
If one takes the histogram for the input image and normalizes it so that the area under the histogram is 1, we have a probability distribution for grey levels in the input image Pr(r).
If we transform the input image to get s = T(r) what is the probability distribution Ps(s) ?
From probability theory it turns out that
![]()
Consider the transformation
![]()
![]()
![]()
Discrete Formulation
We first need to determine the probability distribution of grey levels in the input image. Now
![]()
The transformation now becomes
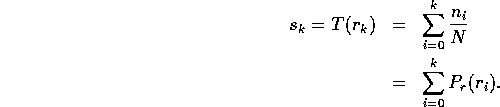
Note that ![]() , the index
, the index
![]() ,and
,and ![]() .
.
The values of sk will have to be scaled up by 255 and rounded to the nearest integer so that the output values of this transformation will range from 0 to 255. Thus the discretization and rounding of sk to the nearest integer will mean that the transformed image will not have a perfectly uniform histogram.