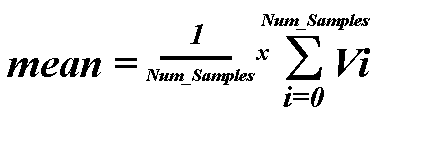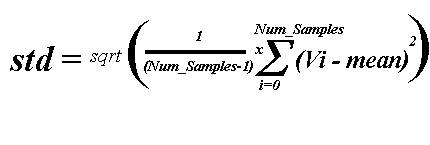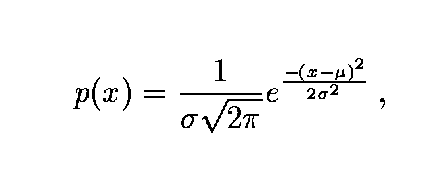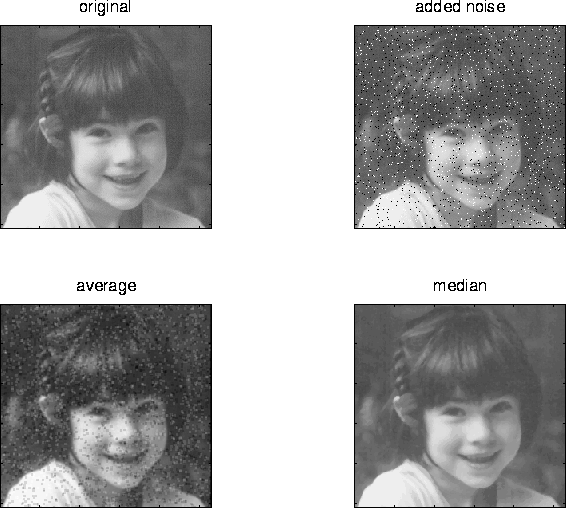Images and Noise
An image signal can have noise introduced at many stages including
digitization, or transmission. There are two types of noise that are of specific
interest in image analysis.
Noise is usually described by its probabilistic characteristics.
- White noise - constant power spectrum (its intensity does not decrease
with increasing frequency); very crude approximation of image noise
- Gaussian noise is a very good approximation of noise that occurs in many
practical cases
- probability density of the random variable is given by the Gaussian curve;
- 1D Gaussian noise - µ is the mean and is the standard deviation of the
random variable.
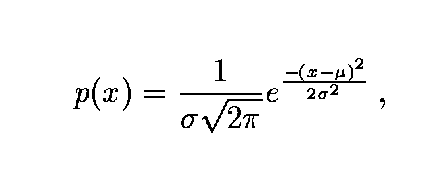
Shot Noise Example
Reducing Noise through Ensembles of Images
Suppose that we take one
picture of a scene, then another, and another, and another. Because of random
variations in light, the random distribution of molecules of air in the path of
the light, the random distribution of silver-halide grains in film, etc., we'll
never quite get exactly the same picture twice.
We can consider the picture, P(r,c) as a random variable from
which we sample an ensemble of images from the space of all possibilities. This
ensemble has a mean (average) image, which we'll denote as Pmean(r,c).
As with most stochastic processes, if we sample enough images, the
ensemble mean approaches the noise-free original signal.
So, one way to often eliminate noise is to take a lot of pictures.
However, this usually isn't feasible.
If we compare the strength of a signal or image (the mean of the
ensemble) to the variance between individual acquired images we get a
signal-to-noise ratio, SNR:
SNR = mean/standard_deviation
A high signal-to-noise ratio indicates a relatively clean signal or image;
a low signal-to-noise ratio indicates that the noise is great enough to impair
our ability to discern the signal in it.
In-Class Assignment/Exercise
The files Orig_N*.jpg contains
a sequence of images corrupted by noise. Average any number (2..4) of
these images together to reduce the noise. Display the result. Why does
this work? How many is enough? How can you tell?
Original Image

|
Reducing Noise through Averaging or Media Filters
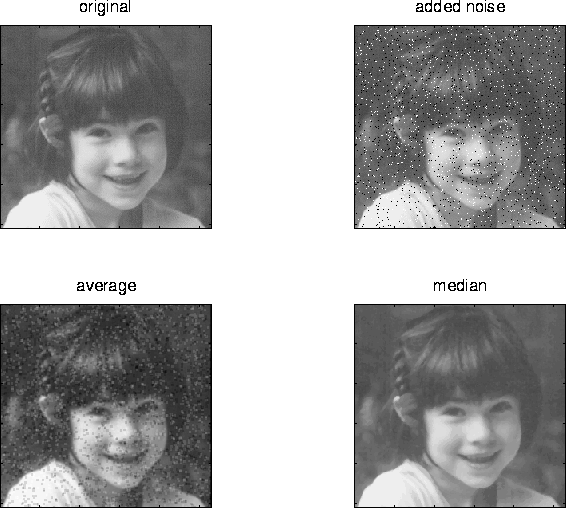
Figure:Original image, w/ salt&pepper
noise, result after averaging/smoothing filter, result after median
filter.