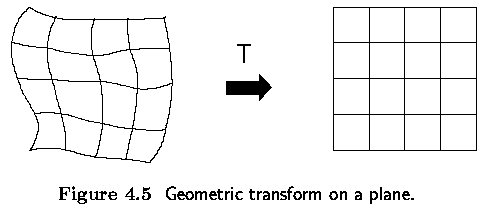
Geometric transformations

![]()
Pixel co-ordinate transformations
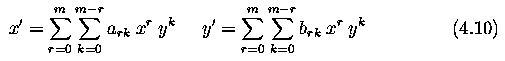

| In-Class Assignment/Exercise Create a set of 20 images that will be used to make up a video sequence. 1) Write a program to has an option to display the 20 images in a loop like a looped video sequence. 2) Perform Decimation on this Sequence in the time domain (down-sample in the time domain) and reduce the number of frames by 10. This is a crude way of performing a form of compression....you are reducing the number of frames. How would you do this? Would you discard every other image in your video sequence? Make this an option in your program and display the results? What does this look like....what has happened? 3)Now perform Interpolation on the decimated video sequence. This will show you how after our simple compression in step 2 we can try to improve the results when played back to the user. Interpolation will now take place in the time domain. We have already seen how to decimate and interpolate in the spatial domain; this extends very naturally to decimating and interpolating in the time domain (decimating and interpolating the image frames). To do this, use a bilinear interpolation scheme to interpolate in between frames. For example, to interpolate the frame between frame1 and frame2, you will be using a triangular kernel centered at frames 1 and 2 at each pixel (this should actually be pretty easy since you are only interpolating by a factor of 2). Display the reinterpolated image sequence and comment on how it compares to the original video sequence. |

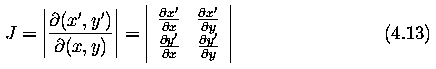
![]()
![]()
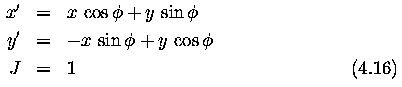
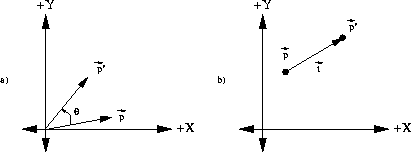
Figure: (a)Anticlockwise rotation of
point p by angle theta, (b) Translation of the point p by the
vector t

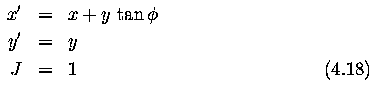
Write a program that rotates an image by a specified angle. The
transformation for rotation by angle t around point (xc, yc) is x' = (x - xc) cos t - (y - yc) sin t + xc y' = (x - xc) sin t + (y - yc) cos t + ycApply your method to the image in 15 degree increments to rotate the image by 120 degrees. Compare this to rotating directly by 120 degrees. What happens? Why? |
![]()
![]()