
Most spatial quantities are represented quantitatively by specifying the quantity relative to a coordinate system. The usual coordinate systems in use are:
The coordinate systems are specified using as many axes as there are dimensions. The axes are usually perpendicular, and there is a ``coordinate system origin'' where all the axes intersect and which has the value (0,0) or (0,0,0), etc, depending on the dimensionality of the space.
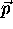

Figure 1a shows
point 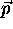 . For simplicity
in text, the vector can also be represented as
. For simplicity
in text, the vector can also be represented as 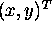 . The T turns
(``transposes'') a vector from a horizontal direction to a vertical direction
and vice versa:
. The T turns
(``transposes'') a vector from a horizontal direction to a vertical direction
and vice versa: 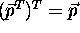 .
.
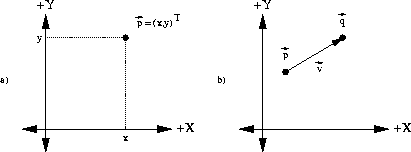
Figure 1: a) Point  in 2D coordinate system. b)
vector
in 2D coordinate system. b)
vector  between points
between points
 and
and 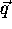
If a vector is 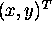 ,
then the length of that vector is:
,
then the length of that vector is:
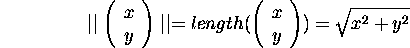
The length of the vector is also called the norm of the vector,
although more properly it should be called the 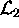 norm or 2-norm, for reasons that
we need not go into here.
norm or 2-norm, for reasons that
we need not go into here.
Vectors can represent directions. In this case, the vector is usually a unit vector, that is, it has length 1. One can create a unit vector by dividing a vector by its length:
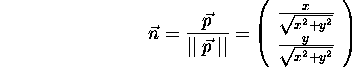
Vectors are added/subtracted by adding/subtracting their components:
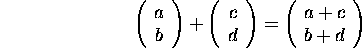
Vectors can represent changes/differences in positions. In this case, the
length of the vector is the distance between the points. If 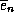 and
and 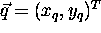 are two point positions, then the
vector
are two point positions, then the
vector 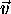 between them
(see Figure 1b) is:
between them
(see Figure 1b) is:
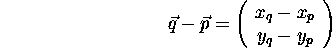
and the distance between the points is the length of the vector between them.
The dot product between two vectors 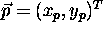 and
and 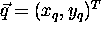 is defined as:
is defined as:

The angle between two vectors is defined using the dot product:
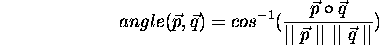

where 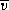 is a vector and V is the space in which it lives.
is a vector and V is the space in which it lives.
For example, vectors in the two-dimensional Cartesian plane like you've seen
in introductory Physics courses have a first component that can be any real
number and a second component that can also be any real number. Using the symbol
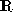 to denote the
set of real numbers, we can describe this vector space as
to denote the
set of real numbers, we can describe this vector space as 
or more compactly, .gif)
By definition, a vector space is closed: linear combination of vectors in the
space always produces another vector in the space. A set of vectors from which
you can construct any other vector in the space is called a
spanning set. For example, by combining some amount of the vectors .gif) ,
, .gif) , and
, and .gif) , one can construct any other vector in the 2-D plane.
, one can construct any other vector in the 2-D plane.
A minimal spanning set (one that contains as few vectors as possible) is called a basis set. In the previous example, one really only needs any two of the three vectors to span the space.
It is useful for the vectors in a basis set to have no components in the
direction of each another (orthogonal). In the previous example, .gif) and
and  are an orthogonal basis set while the other pairs aren't.
are an orthogonal basis set while the other pairs aren't.
Finally, since we're spanning the space through linear combinations of vectors, the actual length of the vectors isn't really important--the direction is. To simplify things, we'll usually work with unit-length vectors for our basis sets. Basis sets that are orthogonal and normalized to unit length are called orthonormal.
A compact way of writing that a set of vectors 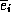 is orthonormal is write
is orthonormal is write

where the function 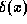 (called the Krönecker delta function) is defined as
(called the Krönecker delta function) is defined as .gif)
Think of this as a mathematician's way of writing ``1 if
they're the same and 0 if they're different''. This is simply a compact notation
for expressing the familiar definition that orthonormal vectors have length one
and are orthogonal to each other.
Notice that a single vector space has an infinite number of possible sets of
basis vectors. The two-dimensional plane can be spanned by .gif) and
and .gif) , or it can be spanned by
, or it can be spanned by .gif) and
and .gif) .
.
We also aren't strictly limited to Cartesian representation of the space. For
example, the 2-D plane can be spanned by the Cartesian vectors .gif) and
and .gif) or by the polar basis vectors
or by the polar basis vectors .gif) and
and .gif) .
.
Conversions from representing a vector space in terms of one set of basis vectors to representing the same space in terms of a different set of basis vectors will be fundamental to later lectures.
Let .gif) ...
...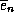 be a set of orthonormal basis vectors for a vector space, then (as we have seen)
any vector v in that space can be represented by
be a set of orthonormal basis vectors for a vector space, then (as we have seen)
any vector v in that space can be represented by
.gif)
and .gif) is the jth element of vector
is the jth element of vector .gif) and
and .gif) [j] is the jth element of vector
[j] is the jth element of vector .gif) .
.
In other words, any vector .gif) is a weighted sum of the basis vectors
is a weighted sum of the basis vectors 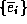 , and the weight
, and the weight 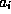 of each vector is
the dot product between the vector v and the basis vector
of each vector is
the dot product between the vector v and the basis vector 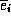 .
.
In this way, any vector can be transformed from a set of components 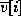 to a set of
components
to a set of
components 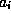 in a coordinate system whose basis vectors are
in a coordinate system whose basis vectors are 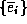 . This is known as a
change of coordinates or a coordinate transformation.
. This is known as a
change of coordinates or a coordinate transformation.
.gif) matrix has N rows and M columns, each entry of which is a number.
An example
matrix has N rows and M columns, each entry of which is a number.
An example .gif) matrix
matrix .gif) is:
is:
.gif)
One often summarizes the notation of a matrix by saying .gif) is
is
.gif) , referring to the
, referring to the 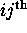 entry of the matrix ( i.e. the entry at the
entry of the matrix ( i.e. the entry at the 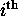 row and
row and 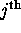 column).
column).
For vision purposes, most arrays are square, meaning that they have the same number of rows and columns.
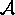 be a
be a 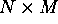 matrix and
matrix and 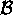 be a
be a 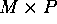 matrix. Then, the matrix
matrix. Then, the matrix
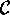 that is their product
is a
that is their product
is a 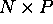 matrix. If
matrix. If 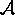 is
is 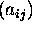 and
and 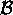 is
is 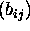 , then the entries of
, then the entries of 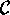 are given by:
are given by:

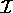 , which is a square matrix
containing all zeros except along the top-left to bottom-right diagonal (called
the main diagonal), which has the value one at each diagonal position.
Here is the
, which is a square matrix
containing all zeros except along the top-left to bottom-right diagonal (called
the main diagonal), which has the value one at each diagonal position.
Here is the 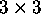 identity
matrix:
identity
matrix:

The identity matrix is a special case of a diagonal matrix, which contains zeros at all locations except along the main diagonal. Here is a diagonal matrix:
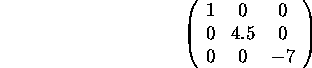
For each matrix  ,
there is a special matrix called the inverse of
,
there is a special matrix called the inverse of  , and is often denoted
, and is often denoted 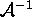 . This matrix has the property:
. This matrix has the property:
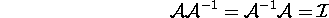
In the case of 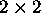 matrices, if the matrix
matrices, if the matrix 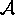 is:
is:

then the inverse of 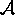 is:
is:
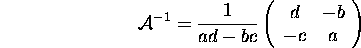
The product of matrices is not commutative, which means that, in general,

(although sometimes they are equal for particular matrices). However, matrix products are associative, which means:

To transform a vector into a new coordinate system, one must thus compute its
projection onto each of the coordinate basis vectors. If there are N
dimensions to the space, this requires N dot products each of the form in
Eq. 3.7.
A compact way of writing this is to write a single matrix A whose
rows are the coordinate basis vectors and take the dot product of each
row of the matrix with the vector to be transformed: .gif)
This operation is multiplication of a vector by a matrix: .gif)
where .gif) is the transformed vector (the weights
is the transformed vector (the weights .gif) ).
).
Suppose that we had a set of vectors that we needed to transform into the
same space. We could put these vectors into a single matrix V whose
columns are the vectors to be transformed and take the dot product of
each column of V with each row of A to give a set of vectors. What
we get is a new matrix .gif) whose columns are the transformed vectors:
whose columns are the transformed vectors: .gif)
To more precisely put it, matrix multiplication is a compact way of transforming a vector into a new coordinate system and is nothing by a collection of dot products. The columns of the first matrix are vectors to be transformed (expressed in the old coordinate system) and the rows of the second matrix are the new coordinate basis vectors (also expressed in the old coordinate system).
One can also do the same thing by transposing each matrix and reversing their
order. (Remember from linear algebra: .gif) .) You will find that their are two distinct camps that span graphics,
image processing, and computer vision: the ``row vector'' people and the
``column vector'' people. It's all a matter of taste really.
.) You will find that their are two distinct camps that span graphics,
image processing, and computer vision: the ``row vector'' people and the
``column vector'' people. It's all a matter of taste really.
Suppose that you wanted to transform a set of vectors into one coordinate
system and then from there into another expressed in terms of the new one. One
can just multiply the matrix of initial vectors by the first transformation
matrix and then multiply the result by the second: .gif)
(Notice that to add a transformation, we add a matrix on the
left side of the existing matrices.) However, matrix multiplication is
associative, so .gif)
This means that the result of the two transformations is the
same as one single transformation whose matrix is the product of the other two.
This is called matrix composition: the collapsing of a set of transformations into a single (usually more complex) one. Notice that for a large set of initial vectors it usually more efficient than applying each transformation successively.