CS6825: Computer Vision word cloud
Instructor Outline Syllabus Projects Links  

Hough Transform

 
 
A technique to find specific points in an image belonging to a specific shape: i.e. lines or circles.
 
You perform a separate transform for each shape you are searching for.
 
 
Given marked edge pixels, find examples of specific shapes Line segments Circles Generalized shapes (GHT)
 
Basic idea - Patented 1962
 
Every edge pixel is a point that votes for all shapes that pass through it.
 
Votes are collected in “parameter space” - look for peaks “Parameter space” is a k-D histogram!
 
 
 

Hough Transform for Lines

 
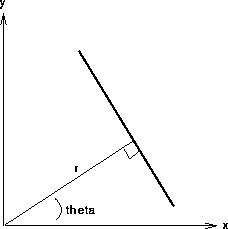
Parameter space: Ax+By+C = 0 (But A,B, C aren’t unique!)
...this is general equation of a line
 
1) Divide by sqrt(A*A+B*B); first two terms are sin,cos of the angle
 
2) Angle, distance from 0
 
3) Angle = arctan(A/B), distance = C/(A*A+B*B)
 
 
 
4) Given a point (x0,y0), find all theta, distance pairs
cos(theta)*x0 + sin(theta)*y0 + distance = 0

5) Increment all “cells” in p-space through which curve passes

 

888888888

 

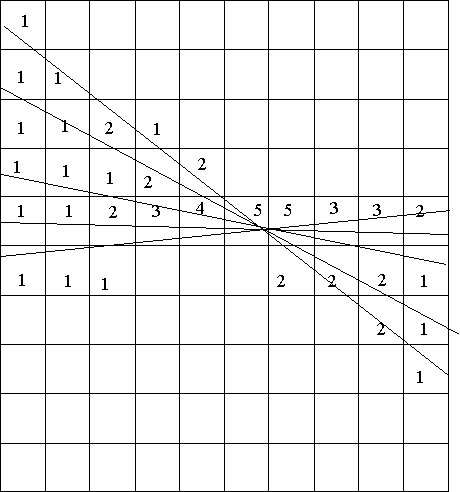
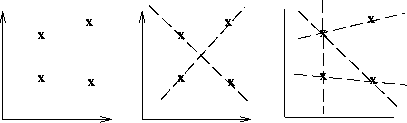
Consider a set of points....(like pixels in an image), how can you possibly fit lines through them....there are multiple possibilities

We can analytically describe a line segment in a number of forms. However, a convenient equation for describing a set of lines uses parametric or normal notion:

such that we have

r, theta are the values that we seek.

 

So,

1) Detect points (e.g. via edge detection) that belong to all of the possible lines in an image

2) For any point in the image (Xi, Yi) there is a set of possible (r,theta) values for which it may belong to. These (r,theta) values are all of the possible lines this point may be part of. So, First

segment the Hough transform space into cells of (r,theta) values

 

3)For each point in the image (Xi, Yi), determine the curve equation with unkowns (r,theta) and increment all of the (r,theta) cells in the discrete Hough transform space the curve intersects.

4) Peaks in the Hough transform space indicate strong evidence of lines with that r,theta. Perform thresholding or take top X% of the peaks to represent the edges in the image.

 

EXAMPLE

Input Image

Edge Detected points

A curve is generated in polar space for each edge point in cartesian space. The accumulator array, when viewed as an intensity image, looks like

r axis----------------------------------------------->

Hough Transform for Circles

 

Parameter space is (centerx, centery, radius)

 

Update: For every point, computer center, radius of all circles passing through the point Mark each center, radius pair

 

Alternative computation: for each cell, compute distance from that cell to point - increment if close enough.

 

8888888

Here the equations is

where a,b and r are the unknowns that we are searching for.

Hence, we have a 3D Hough transform space.

 

Generalized Hough Transform

 

Parameters are translation, rotation & scale of a fixed 2D shape,represented as a point set

 

Given a point and a location in the transform space, if the point is in (or close enough to a point in) the transformed point set, then record a vote.

 
© Lynne Grewe