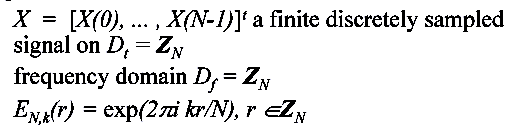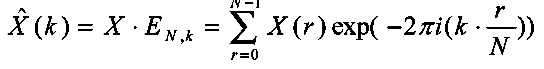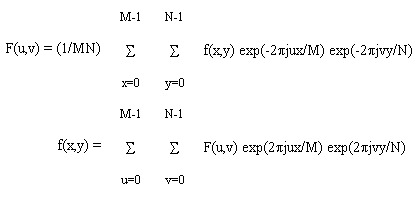The Fourier Transform

Basic Idea:

Any signal can be expressed as a sum of cosine and sine functions.

• the cosine and sine functions are at different frequencies
• this representation is called the Fourier Transform

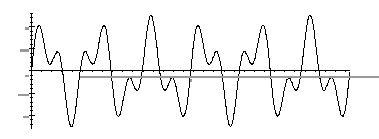
                      x(t) = .75 sin(3t) + .5 sin(7t)

                 Signal                                        Fourier Transform

           Signal                                                       Fourier (magnatude)

Specifics

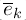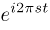• the orthonormal basis vectors for Fourier Transform {} are the set of exponential functions: where s takes on a different value for each basis function and represents frequency.


• You may recall, 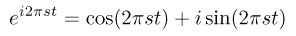which is what is called a "complex number" where the cosine is the "real part" and the sine is the "imaginary part" of the real number.
  
  
  
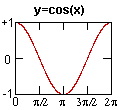
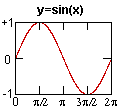  These are periodic signals, that keep repeating. The smaller the distance between peaks, means a higher frequency signal. Think of this distance as the wavelength. (1/length proportional to frequency)
  
  
• Hence we have for the forward and inverse of the Fourier Transform.

Discrete Fourier Transform: DFT

2D DFT of a 2D digital image

where f(x,y) is the 2D image (x, y) is a pixel location

F(u,v) is the transformed image (u,v) is a pixel location in the Frequency Domain. (u,v) represent frequencies...hence (0,0) is the DC component meaning no frequency in either the horizontal or vertical directions.

The Fourier Transform produces a complex number valued output image which can be displayed with two images, either with the real and imaginary part or with magnitude and phase. In image processing, often only the magnitude of the Fourier Transform is displayed, as it contains most of the information of the geometric structure of the spatial domain image. However, if we want to re-transform the Fourier image into the correct spatial domain after some processing in the frequency domain, we must make sure to preserve both magnitude and phase of the Fourier image.

Image                          Magnatude               Phase

Inverted-No Mag         Inverted- No Phase

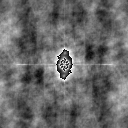
Image

Fourier Magnitude

Fourier Phase

2D FFT - Fast Fourier Transform

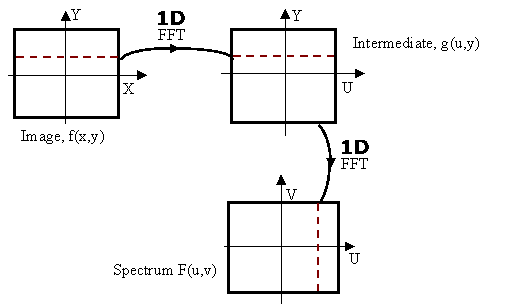
A fast algorithm (FFT) is available for computing this transform, providing that N and M are powers of 2. In fact, a two dimensional transform can be separated into a series of one dimensional transforms. In other words, we transform each horizontal line of the image individually to yield an intermediate form in which the horizontal axis is frequency (u) and the vertical axis is space (y). We then transform individually each vertical line of this intermediate image to obtain each vertical line of the transformed image. Hence a two dimensional transform with of an n by n image consists of 2n one dimensional transforms as follows:

A Few Features of Frequency Domain:

• Many times a complex signal in the spatial domain will transform to a more simple frequency signal.
  

  Hence, you could choose to store the frequency signal instead of the spatial signal to save space.....COMPRESSION. Then simply take the inverse transform whenever you want to view the original spatial signal.

  Lynne's Generality: Usually, the more complex a picture is, the more savings you may have when representing it in the frequency domain.

  

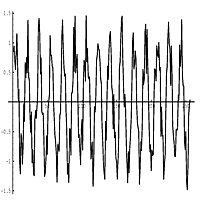
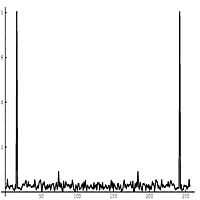
             Signal                          Fourier Transform

  
                Signal                           Fourier (magnatude)
  

• Can create all kinds of filters in the Fourier Frequency domain to smooth (low-pass...keep lower frequencies) or sharpening (emphasize higher frequencies) or edge detection (high-pass...keep higher frequencies).
  
  
  
• Magnatude of Fequency signal called Spectrum Magantude is invariant to translation. Can use in template matching and do not have to worry unlike in Spatial domain about translation of pattern.
  
  

  Correlation with a template can be done in one pointwise multiply of the spectrum magnitudes with the template spectrum magnitudes. Thus for a set of templates, whose spectra we can pre-calculate, we can very quickly find the best match, and the size of the correlation tells us whether the template matches at all. This is compuationally much more efficient than doing a correlation by trying the template at all possible positions in spatial domain. Moreover, the position of a matched template in the spatial domain can be deduced from the phase (ratio of since to cosine components in the spectrum) of the fundamental.