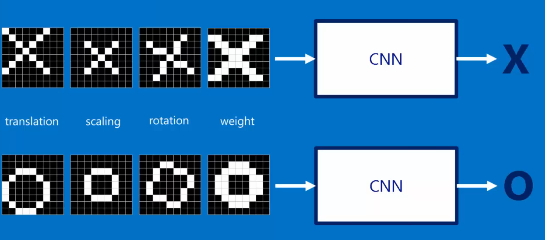
Example to Understand CNN - determine if image has X or O

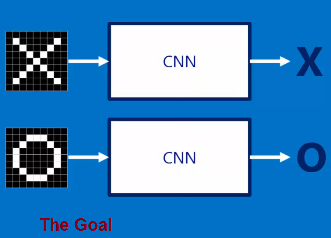
The Input = raw image

Training --need LOTS LOTS of examples (training data)

How much training data --- examples for some forms of object recognition - could go into 100,000 samples or more. Sometimes like 10,000 or maybe for the really really simple example we show here we might get away with 200?

Motivation/Explanation - why CNN for this kind of Raw data NN.....taken from https://www.youtube.com/watch?v=FmpDIaiMIeA

 

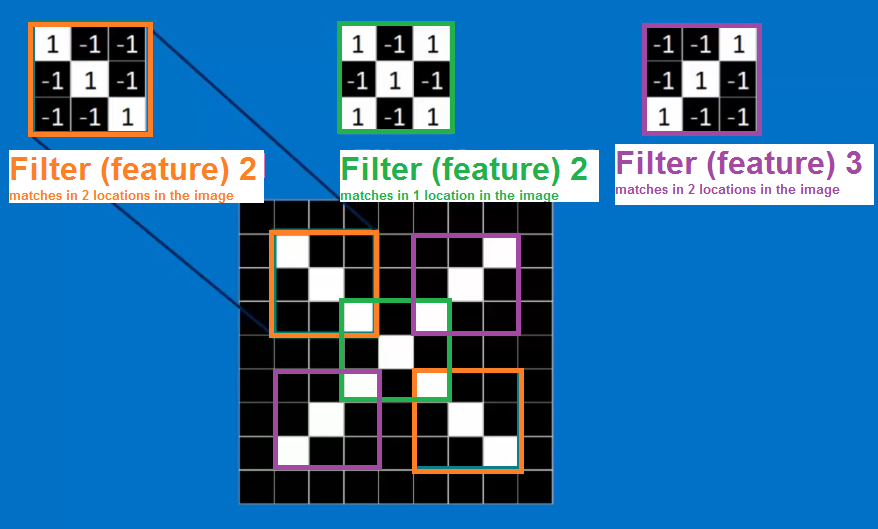
CNN --- in "some way" can be thought of breaking it down and matching parts of image to each other ---

• The matching is done through convolving the image with the MxM mask/filter
  
  
  

QUESTION: How many Filters do we apply at each level?????? ---here we show 3 filters/masks

RESULTS

These MxM filters/masks are applied convolutionally at each layer in our CNN - in the case of our input image we apply this at each raw input pixel (at each red, green, blue if color) and we can apply only 1 MxM filter or could have multiple filters like shown above the case is 3 -- in our binary image input this would result in 3 times the amount of input data for the 3 images.......

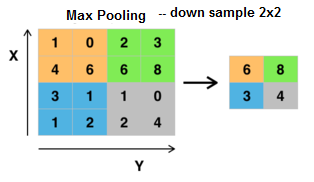
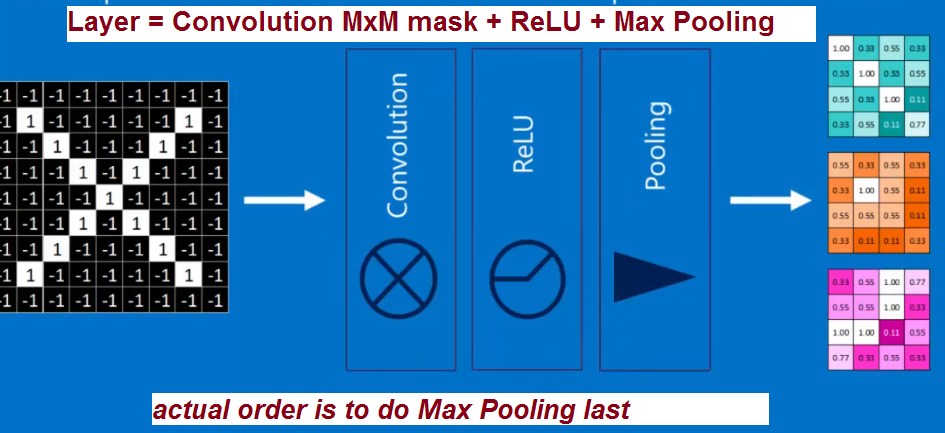
<< example where input image 32x32 pixels and have THREE MxM filters convolve with yielding 6 times data. Note here MxM =5x5 and we can not convolve with the first 2 and last 2 rows and columns (boundaries of image) --> so get THREE 28x28 size data values ---- YIKES bigger --- I want the output 2 have 2 nodes "X" and "Y". What am I going to do??? --> CNN does downsampling at each layer called Max Pooling

 

MAX Pooling - typically do on 2x2 (or maybe 3x3)

NOW we have THREE 14x14 data sets --thats a bit better

RESULTS

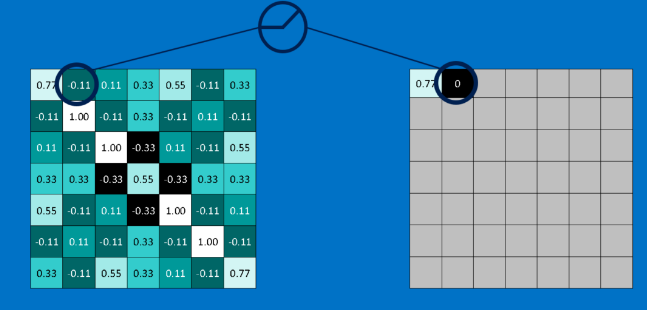
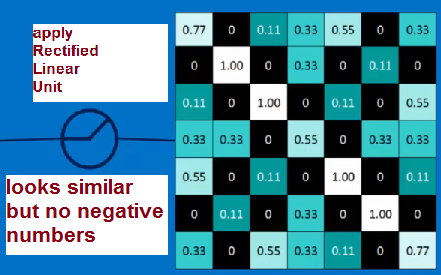
WAIT we not done --- we must introduce a non-linearity and do so for CNN at each data sample by applying Rectified Linear Units: set values < 0 to 0

LAYER = Convolution with set of (1-*) MxM filters + nonlinear + max pooling (downsample)

 

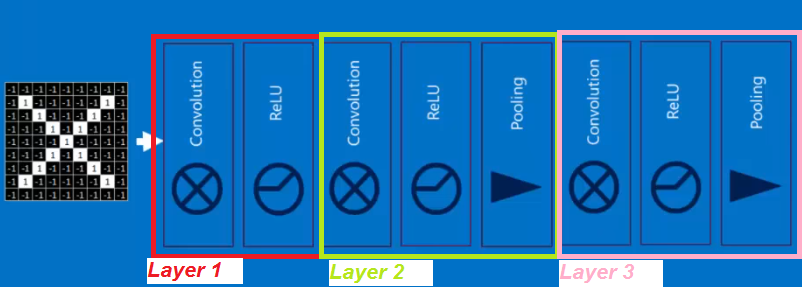
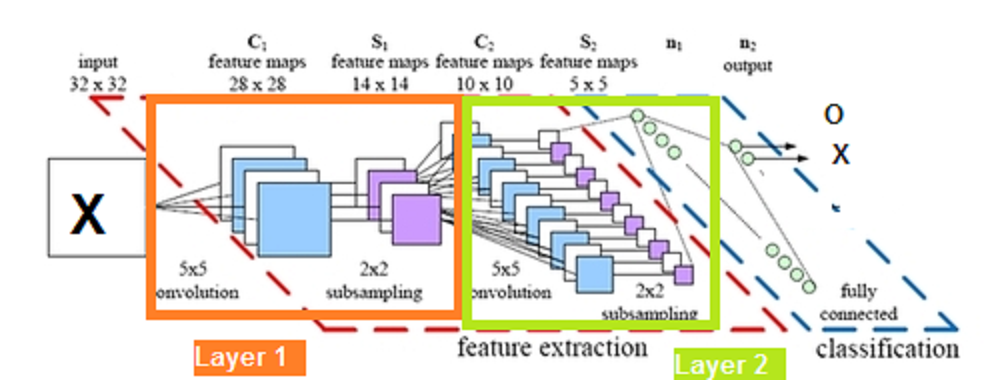
Example with 3 Layers using convolution masks

 

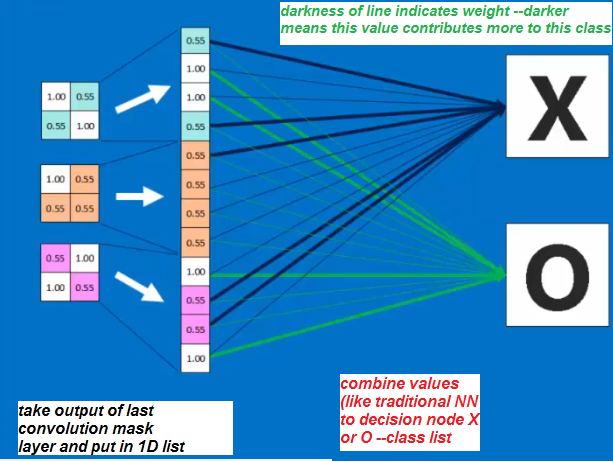
Last Layer -decision Layer (you can have more than one layer at the end that is fully connected like this --but, minimum is 1)

After Training --making the decision at last layer

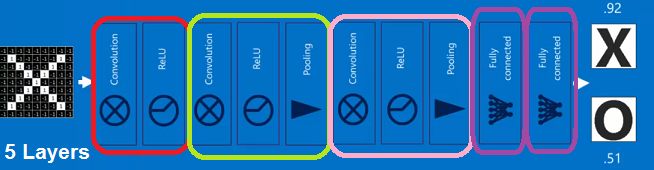
So here is final structure of a CNN we might use for our X,O recognition

HERE is another possible smaller CNN for our problem- 3 Layer example --2 layers with convolution masks and the last layer is fully connected nodes yielding decision X or O

Questions: How many Layers? How many masks at each layer? What is size of masks? Which masks? What are the weights in the Fully connected layers? Generally not learned -you set, Generally learned ....there are more questions

• Question 1: How many layers of each type (convolution and fully connected)?

hard to answer - minimum 3 largest maybe 6-15 (but, that is changing) . For sure the more layers, the longer to train and in general more data needed. More complex the problem more layers. Simpler the problem less layers needed. Minimum 1 fully connected layer. NOT LEARNED, you decide

• Question 2: How many masks at each layer?

hard to answer - could learn this. Minimum obviously 1. NOT LEARNED, you decide

 

• Question 3: what size is the mask?

hard to answer - minimum is 3x3. Could be larger but, should not exceed 25% of image (?? of thumb). larger mask means larger scale pattern looking to match via convolution. NOT LEARNED, you decide

 

• Question 4: What is content of MxM mask?

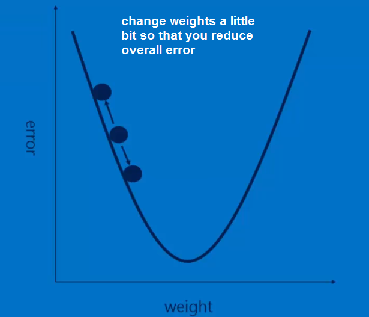
you learn this through training (backpropogation like traditional NN, use error between output and desired output to alter the parameters) LEARNED

 

• Question 5: What are the weights in the fully connected layers?

you learn this through training (backpropogation like traditional NN, use error between output and desired output to alter the parameters) LEARNED

A different example --detection of faces with input RGB. Different filters (and number) at each layer are applied

OUTCOME: CNN capture "local" spatial patterns at different scales (downsampling-max pooling) --- good for Image Applications