|
||||||
|
Huffman Coding
Coding- is the process of assigning codes to a set of symbols (this may be numbers themselfs)possibly for the goal of compression (encription is another application). The idea hear is that replacing the symbols by their codes will result in a smaller data set.
Huffman Coding
- This is a coding procedure that uses a tree data structure to assign the codes.
- Also uses probabilty of the occurance of a symbol to determine whether it recieves a long or short code. The higher the probability that a symbol will occur means it will be assigned a shorter code.
- Code consists of a series of 1's and 0's.
1. Initialization: Put all the symbols in an OPEN list, keep it sorted at all
times (e.g., ABCDE). In our case the symbols will not be letters but,
actually number representing the greylevel or color values of the pixels in an
image
OPEN = {A B C D E}
2. Create the bottom of a tree structure and assign each element in OPEN to a node at this level of the tree.
3. Repeat until the OPEN list has only one node left:
(a) From OPEN pick two nodes having the lowest frequencies/probabilities,
create a parent node of them.
(b) Assign the sum of the children's
frequencies/probabilities to the parent node and insert it into OPEN.
(c)
Assign code 0, 1 to the two branches of the tree, and delete the children from
OPEN.
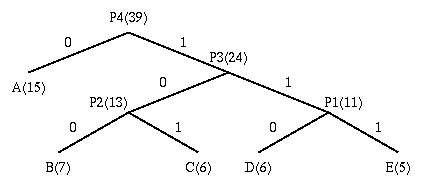
The resulting Codebook (assignment of codes to input symbols)
Symbol Count log(1/p) Code Subtotal (# of bits)
------ ----- -------- --------- --------------------
A 15 1.38 0 15
B 7 2.48 100 21
C 6 2.70 101 18
D 6 2.70 110 18
E 5 2.96 111 15
TOTAL (# of bits): 87
Discussions:
- Decoding (given a code, determine the original symbol) for the above algorithms is trivial as long as the coding table (the statistics) is sent before the data. (There is a bit overhead for sending this, negligible if the data file is big.)
- Unique Prefix Property: no code is a prefix to any other code (all
symbols are at the leaf nodes)
--> great for decoder, unambiguous. - If prior statistics are available and accurate, then Huffman coding is very good.
In the above example:
entropy = (15 x 1.38 + 7 x 2.48 + 6 x 2.7 + 6 x 2.7 + 5 x 2.96) / 39
= 85.26 / 39 = 2.19
(Entropy is a measure of information)
Average Number of bits needed for Human Coding is: 87 / 39 = 2.23
Adaptive Huffman Coding
Motivations:(a) The previous algorithms require the statistical knowledge which is often
not available (e.g., live audio, video).
(b) Even when it is available, it
could be a heavy overhead especially when many tables had to be sent when a
non-order0 model is used, i.e. taking into account the impact of the previous
symbol to the probability of the current symbol (e.g., "qu" often come together,
...).
The solution is to use adaptive algorithms. As an example, the Adaptive Huffman Coding is examined below. The idea is however applicable to other adaptive compression algorithms.
ENCODER DECODER
------- -------
Initialize_model(); Initialize_model();
while ((c = getc (input)) != eof) while ((c = decode (input)) != eof)
{ {
encode (c, output); putc (c, output);
update_model (c); update_model (c);
} }
Summary
- Huffman maps fixed length symbols to variable length codes. Optimal only when symbol probabilities are powers of 2.
- Lempel-Ziv-Welch is a dictionary-based compression method. It maps a variable number of symbols to a fixed length code.
- Adaptive algorithms do not need a priori estimation of probabilities, they are more useful in real applications.
