Motivation

How can we implement a table?

• need insert, delete and search operations

A1) Sorted Array

Binary search is fast O(log(N))

Delete and Insert require O(N) steps

A2) Linked List

Search is slow O(N)

Insert and delete are fast, once we find the right spot

 

Goal

Is there a datastructure to support O(log(N)) search, insert and delete operations?

 

Problem with Linked List: in search only one path to take.....

what if we had more than one path (link)

Solution: Tree???

Best Case: Fast

Worst Case: Like a Linked List

Better Solution: Constrained Trees (e.g. Binary Tree)

 

 

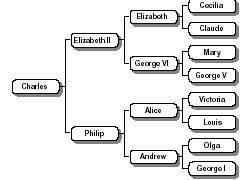
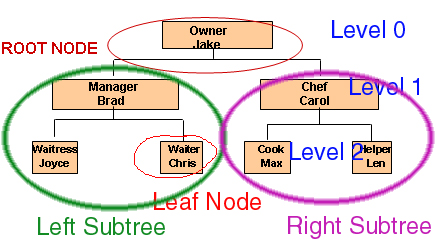
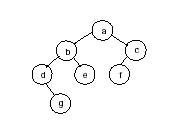
Examples of Binary Trees

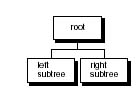
Tree is either empty or has a node containing information

and a left and right sub-tree.

The Binary Search Tree

A special kind of binary tree in which:

1. Each node contains a distinct data value

2. The key values in the tree can be compared using “greater than” and “less than”

3. The key value of each node in the tree is less than every key value in its right subtree, and greater than every key value in its left subtree.

Implementing Trees with Pointers and dynamic memory

Example Creation of a BST ----order is important

Traversal of a Binary Tree

	PostOrder left, right, then root g d e b | f c | a
	InOrder left, root, then right d g b e | a | f c
	PreOrder root, left, then right a | b d g e | c f

Binary Tree Search                Tree Insertion               Tree Deletion

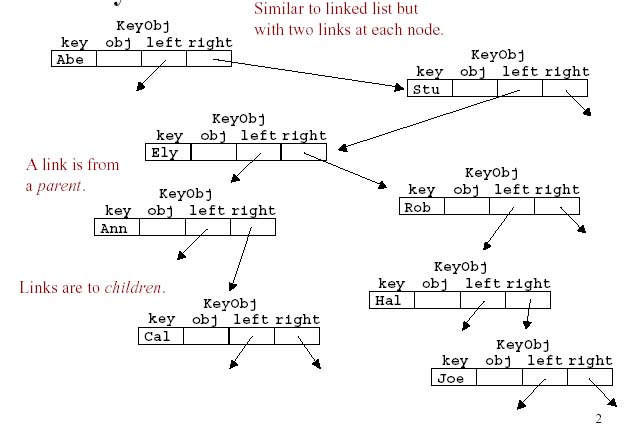
Some Code to represent a BST

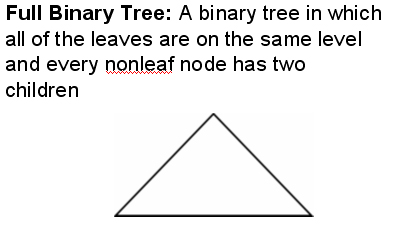
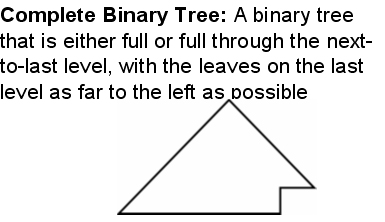
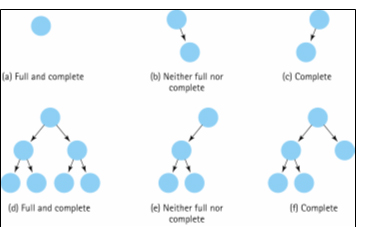
Some Terms