CS3240: Data Structures and Algorithms

B-Tree

• Generalized version of Binary Search Tree --- which can have MORE THAN 2 CHILDREN

  • can have a variable number of child nodes within some pre-defined range

  • number of child nodes changes when nodes inserted or deleted

  • Because a range of child nodes is permitted, B-trees do not need re-balancing as frequently as other self-balancing search trees, but may waste some space, since nodes are not entirely full.

  • The lower and upper bounds on the number of child nodes are typically fixed for a particular implementation. For example, in a 2-3 B-tree (often simply referred to as a 2-3 tree), each internal node may have only 2 or 3 child nodes.

   

• O(log(n)) for searches, sequential access, insertions, and deletions.

   

• Used in systems that read and write large blocks of data --- like databases and filesystems.

  • EXAMPLE: A B-tree is a method of placing and locating files (called records or keys) in a database.

   

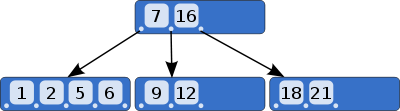
• order = maximum number of children nodes at any node

MORE DETAILS

• Keys = stored at each node are the keys that seperate the child node records.

  • key 1 = all keys in child 1 are < key 1 AND all keys in child 2 are > key 1
  • key 2 = all keys in child 2 are <key 2 AND all keys in child 3 are > key 2
  • key j = all keys in child j are < key j AND all keys in child j+1 are > key j
    
    
• Leaf Nodes = required to be at same depth

See at the root we first have the key 7 as it separates its first child (keys containing 1,2,5,6) from its second child (keys containing 9,12) and the root's second key is 16 seperating its second child (keys 9,12) and its 3rd child (keys 18 and 21).

Lets put it all together

1.  the number of keys in each non-leaf node is one less than the number of its children and these keys partition the keys in the children in the fashion of a search tree

2.  all leaves are on the same level

3.  all non-leaf nodes except the root have at least ceiling(m / 2) children

4. root = a leaf node, or it has from two to m children

5.  a leaf node contains no more than m – 1 keys