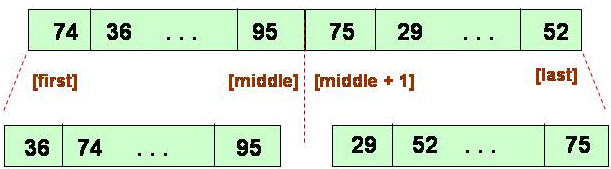
MergeSort Algorithm
1) Cut the array in half.2) Sort the left half.3) Sort the right half.4) Merge the two sorted halves into one sorted array. |
// CODE // Recursive merge sort algorithm template |
Running Time
MergeSort is O(N*logN). |