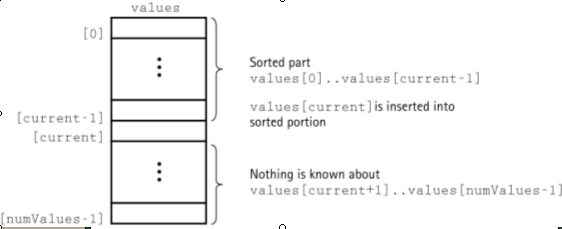
InsertionSort Algorithm
|
On each pass, this causes the number of already sorted elements to increase by one.
Snapshot of InsertionSort
|
// CODE template |
Running TimeThis algorithm is O(N^2).
|
 One
by one, each as yet unsorted array element is inserted into its
proper place with respect to the already sorted elements.
One
by one, each as yet unsorted array element is inserted into its
proper place with respect to the already sorted elements. 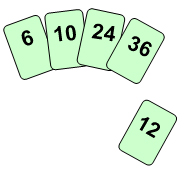 Works
like someone who “inserts” one more card at a time into a hand of
cards that are already sorted.
Works
like someone who “inserts” one more card at a time into a hand of
cards that are already sorted. 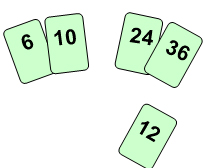 To
insert 12, we need to make room for it by moving first 36 and then
24.
To
insert 12, we need to make room for it by moving first 36 and then
24.