Objective

• Take a list of elements and put them in order, i.e. sort them.

Suppose we have the following array and we wish to sort them using quicksort algorithm

Idea:

1) we can select the first item in the list and use it as a "Split Value" to split the list in 2...where by everything on the left of the list is < this Split Value and everything on the right is >= this SplitValue.

2)then we recursively call split on the two lists, on the left and right of the split value.

Recurisive Algorithm

// Recursive quick sort algorithm
//PSUEDO CODE!!!!!!!!!!!!!!!
 
template <class  ItemType >
void  QuickSort ( ItemType A[ ] ,  int first, int  last )	
	
//  Pre:   first <= last
//  Post: Sorts array A[ first. .last ] into 
//  ascending order
{
	if ( first < last )                    //  general case

	{ int splitPoint;

     splitPoint = Split ( A, first, last) ;		

	  // A[ first ] . . A[splitPoint - 1 ] <= splitVal
	  // A[ splitPoint ] = splitVal
	  // A[ splitPoint + 1 ] . . A[ last ] > splitVal

	  QuickSort( A,  first,  splitPoint - 1 ) ;
	  QuickSort( A,  splitPoint + 1,  last );
	}
           
} 



//PSUEDO CODE !!!!
Split(A, first, last)
{	
     splitVal =  A[first];   //use first element as splitVal
     i = first;  //counter starting at first
 

     for(j=first+1 thru last)
       {    if(A[j] <= splitval)
             {  i= i +1; 
                //swap new A[i] with A[j]
                temp = A[j];
                A[j] = A[i];
                A[i] = temp;
              }
       }

     //now swap A[first](contains splitVal) with A[i]
     temp = A[i];
     A[i] = A[first];
     A[first] = A[i];
      
     //return new splitPoint location, the location of splitVal
     return i;
}
            



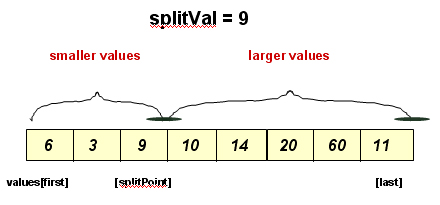
//RESULTS During First call to SPlit
Split(A, 0, 7)

1) A = [9 20 6 10 14 3 60 11 ],
   splitVal = 9, splitPoint = 0 (first position)

2) After first for loop  i = 0, j=2
   A = [9 20 6 10 14 3 60 11]

3) After second for loop  i=1   , j=3
   A = [9 6 20 10 14 3 60 11]

4) After 3rd for loop i=1  , j=4
   A = [9 6 20 10 14 3 60 11]

5) After 4th for loop i=1,j=5
   A = [9 6 20 10 14 3 60 11]

6) After 5th for loop i=2 , j=6
   A = [9 6 3 10 14 20 60 11]

7) After 6th for loop i=2, j=7
   A = [9 6 3 10 14 20 60 11]

8) After 7th for loop i=2, j=8
   A = [9 6 3 10 14 20 60 11]

9) DONE - as j is past last
   //now swap A[first] and A[i]
   A = [3 6 9 10 14 20 60 11]
   splitPoint = i = 2

NOW WE MUST Call QuickSort Recursively
On the 2 sub arrays to left and right of SplitPoint that
Need sorting
QuickSort(A, 0, 1)
QuickSort(A, 3, 7)
            

CONCEPT OF SPLIT

....at any one time in the the For loop of Split have

Any A[x]  where x <=i MEANS A[x] <=splitVal
Any A[x]  where x > i AND x < j  MEANS A[x] > splitVal
Any A[x]  where x >= j MEANS A[x] = yet unknown (not looked at)

[ splitVal  LLLLLL   GGGGGG   UUUUU]

VERY EFFICIENT WITH SPACE!!!!
AN "IN PLACE ALGORITHM"

Running Time

It depends on the order of the original array elements!

If each split divides the subarray approximately in half,

BEST CASE

• there will be only logN splits
• QuickSort is O(N*logN).

 

But, if the original array was sorted to begin with, the recursive calls will split up the array into parts of unequal length, with one part empty, and the other part containing all the rest of the array except for split value itself.

WORST CASE

• In this case, there can be as many as N-1 splits
• QuickSort is O(N^2).

HOW CAN WE MAKE AVERAGE CASE = BEST CASE?

answer 1: radomize / scatter input in array to make "sure" not an ordered array

answer 2: change code and randomize the splitPoint you start with --- swap it initally with first some RADOMLY selected value between first and last before for loop of split.

SOLUTION: RANDOMIZED Quicksort Algorithm

 

THIS is a technique used in computer science to try to avoid sorted input data.