Priority Queue
|
 |
Implementation Possibilities
|
Implementation using Heap
Dequeue = to read root value (highest priority) and remove it
Enqueue = to insert new element in queue
//PSEUDO-CODE
class FullPQ(){};
class EmptyPQ(){};
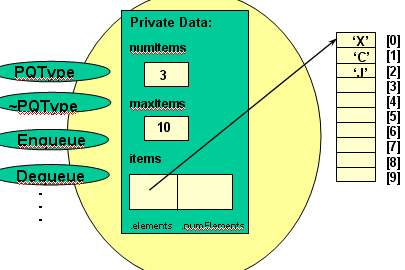
class PQType
{
public:
PQType(int);
~PQType();
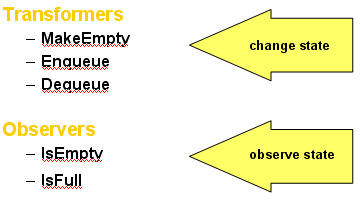
void MakeEmpty();
bool IsEmpty() const;
bool IsFull() const;
void Enqueue(ItemType newItem);
void Dequeue(ItemType& item);
private:
Heap heap;
};
PQType::PQType(int max)
{
maxItems = max;
heap = new Heap();
heap.heapsize = 0;
}
void PQType::MakeEmpty()
{
heap.heapsize = 0;
}
PQType::~PQType()
{
delete [] heap.elements;
}
float PQType::Dequeue() {
if (heap.ISEmpty())
throw(EMPTYHEAP);
max = heap.getRoot(); //first element, root
//put last element at root
heap.setRoot(heap.elements[heapsize]);
heap.heapsize -=1;
Heapify(heap.elements,1);
return max;
}
float PQType::Enqueue(float new_value)
heap.heapsize = heap.heapsize + 1;
index = A.heapsize;
while (index > 1 && heap.getParent(index) < new_value )
{heap.elements[index] = heap.getParent(index);
index = parent(index); //get parent's index
}
heap.elements[index] = new_value;
}
|
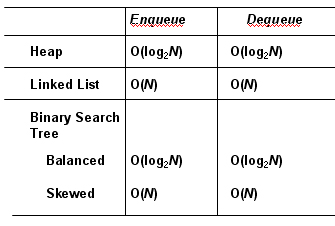 Comparison
of Implmentations......>
Comparison
of Implmentations......>