Optimization
Find values of the variables that minimize
or maximize the objective function
while satisfying the constraints.
objective function
- function we wish to minimize/maximize
- expression of problem as a minimization/maximization
problem.
- Examples
- in a manufacturing process,
we might want to maximize the profit or minimize
the cost.
- In fitting experimental
data to a user-defined model, we might minimize
the total deviation of observed data from predictions
based on the model.
- In designing an automobile
panel, we might want to maximize the strength.
- multiple objectives: Sometimes we would actually
like to optimize a number of different objectives at
once.
- For instance, in the panel design problem, it
would be nice to minimize weight and maximize strength
simultaneously.
- Usually, the different objectives are not compatible;
the variables that optimize one objective may be
far from optimal for the others.
- In practice, problems with multiple objectives
are reformulated as single-objective problems by
either forming a weighted combination of the different
objectives or else replacing some of the objectives
by constraints.
|
variables of objective function
- These are the paramters we alter to achieve the min/max
of the function.
- They become the best, "optimum"
values to solve our problem
- Examples
- In the manufacturing
problem, the variables might include the amounts
of different resources used or the time spent on
each activity.
- In fitting-the-data problem,
the unknowns are the parameters that define the
model.
- In the panel design problem,
the variables used define the shape and dimensions
of the panel.
|
constraints
- these are rules that allow the variables to take on
certain values but exclude others.
- do not necessarily have to have constraints.
- Examples:
- For the manufacturing
problem, it does not make sense to spend a negative
amount of time on any activity, so we constrain
all the "time" variables to be non-negative.
- In the panel design
problem, we would probably want to limit the weight
of the product and to constrain its shape.
|
|
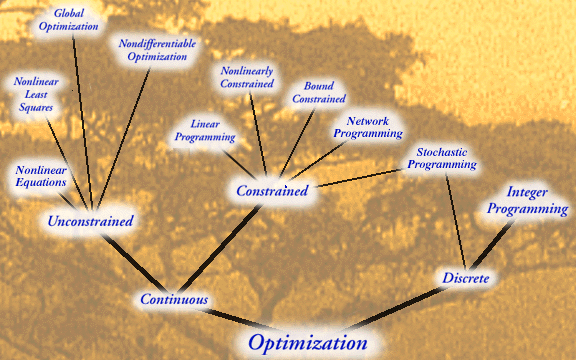
Some Terms
Continuous Optimization: variables are allowed to take
values from subintervals of the real line;
Discrete Optimization: require variables to have integer
values.
Multi-Objective Optimization: optimize
a number of different objectives at the same time.
NEOS Guide to Optimizaton
|
| |
|