Data Structures & Algorithms

Dijkstra's Shortest Path Algorithm

The router based on information that has been collected from other routers, builds a graph of network. This graph shows the location of routers in network and their links. Also every link will be labeled with a number which is called weight of link and is also known as cost of link.

This number is a function of delay time, average traffic and sometimes simply, it is the number of hops between nodes. For example if there were two links between a node to destination, the router chooses the link with the least weight.

The router builds a graph of network and identifies source and destination nodes as V1 and V2 for example. Then it will build a matrix named "Adjacency Matrix”. In this matrix a [i, j] is a weight of link between Vi and Vj .if there was not a direct link between Vi and Vj this amount will be assumed as Infinity.
It builds a status record set for every node of network that contains three fields:
- The first field that shows the previous node. We call this field "predecessor" field.
- The second filed that shows the sum of weights from source to that node. We call this field "Length" field.
- The last field that shows the status of node. Each node can have one status mode: "Permanent" or "Tentative". We call this filed as "Label" filed.
It initializes the parameters of status record set (for all nodes) and set their length to Infinity, and their label as tentative.
Assume V1 as t node and make its label as permanent. Note that when a label changes to permanent, it never changes again. T node just rules as an agent and noting more.
For all tentative nodes that are directly linked to t node, status record set should be updated.
From all the tentative nodes, choose the one whose weight to V1 is less and set it as t node.
If this node is not V2 (destination) then, go to step 5
If this node is V2 then extract its previous node from status record set and do this until return to V1.The nodes show the best route from V1 to V2.

link to Applet DEMO

Example of using Dijkstra algorithm:
Here we want to find the best route between A and E. (See figure 3) You can see that there are 6 possible routes between A and E (ABE, ACE, ABDE, ACDE, ABDCE, ACDBE) and its obvious that ABDE is the best route because its weight is less than other routes. But life is not always so easy and there are some complicated cases in which we have to use algorithms to find the best route.

1-As you see in figure 2,the Source node (A) has been chosen as t node and so its label is permanent (we show permanent nodes with filled circles and t nodes with --> mark)

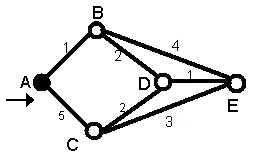
Figure 2

2-In this step you see that status record set of tentative nodes that have a direct link to t node, (B, C), has been changed. Also since B has less weight, it has been chosen as t node and so its label has changed to permanent. (See figure 3)

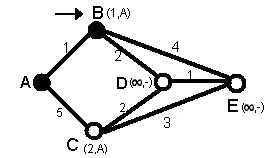
Figure 3

3-In this step like step 2,the status record set of tentative nodes that have a direct link to t node, (D, E), has been changed. Also since D has less weight, it has been chosen as t node and so its label has changed to permanent (See figure 4)

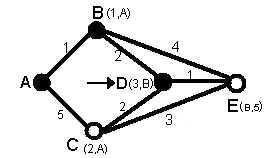
Figure 4

4-Here we don’t have any tentative node so we should just identify the next t node. Since E has the least weight, it has been chosen as t node.

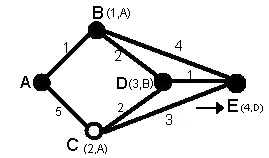
Figure 5

5-E is the destination, so we shouldn't continue. We are at end! So we have to identify the route. The previous node of E is D and previous node of D is B and its previous node is A. So the best route is ABDE. In this case the total weigh is 4 (1+2+1=4).
Although this algorithm works well, its so complicated that may take long time for routers to process it and so the efficiency of network fails. Also if a router gives wrong information to other routers, all routing decisions will be ineffective.
you can see the source of program written by C to understand this algorithm better:

#define MAX_NODES 1024                  /* maximum number of nodes */
#define INFINITY 1000000000           /* a number larger than every maximum path */
int n,dist[MAX_NODES][MAX_NODES]; /*dist[I][j] is the distance from i to j */
void shortest_path(int s,int t,int path[ ])
{struct state {                                               /* the path being worked on */
int predecessor ;                                          /*previous node */
int length                                                      /*length from source to this node*/
enum {permanent, tentative} label                 /*label state*/
}state[MAX_NODES];
int I, k, min;
struct state *
                    p;
for (p=&state[0];p<&state[n];p++){             /*initialize state*/
p->predecessor=-1
p->length=INFINITY
p->label=tentative;
}
state[t].length=0; state[t].label=permanent ;
k=t ;                                                              /*k is the initial working node */
do{                                                                /* is the better path from k? */
for I=0; I<n; I++)                                            /*this graph has n nodes */
if (dist[k][I] !=0 && state[I].label==tentative){
           if (state[k].length+dist[k][I]<state[I].length){
               state[I].predecessor=k;
               state[I].length=state[k].length + dist[k][I]
            }
}
/* Find the tentatively labeled node with the smallest label. */
k=0;min=INFINITY;
for (I=0;I<n;I++)
      if(state[I].label==tentative && state[I].length <
min)=state[I].length;
     k=I;
   }
state[k].label=permanent
}while (k!=s);
/*Copy the path into output array*/
I=0;k=0
Do{path[I++]=k;k=state[k].predecessor;} while (k>=0);
}