|
Problem
with DV Algorithm: Count to Infinity
Let us examine this problem with an example:
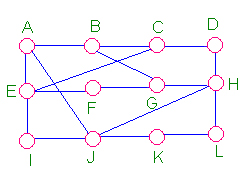
Imagine a network with a graph that has been shown in the
figure below with its Routing table. As you see in this graph,
there is only one link between A and other parts of network.
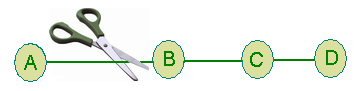
| |
A |
B |
C |
D |
| A |
0,- |
1,A |
2,B |
3,C |
| B |
1,B |
0,- |
2,C |
3,D |
| C |
2,B |
1,C |
0,- |
1,C |
| D |
3,B |
2,C |
1,D |
0,- |
Now imagine that the link between A and
B cut. At this time B corrects its table. After specific
amount of time, routers exchange their tables and so B receive
C's routing table. Since C doesn’t
know what has been happened to link between A and B, its table
says that it has a link to A with the weight of 2. (1 for
C to B and 1 for B to A, because it doesn't know B has no
link to A) B receives this table and thinks there is a separate
link between C and A, so it corrects its table and changes
infinity to 3 (1 for B to C and 2 for C to A, as C said).
After a time again routers exchange their routing table.
When C receives B' routing table it see that B has changed
weight of its link to A from 1 to 3,so it updates its table
and changes the weight of link to A to 4 (1 for C to B and
3 for B to A, as B said). This process loops until all nodes
find out that the weight of link to A is infinity. This situation
is shown in figure 8.In this way experts say DV algorithms
have a slow convergence rate.
| |
B |
C |
D |
| Sum of the weight to A after link cut
|
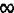 ,A ,A |
2,B |
3,C |
| Sum of the weight to A after first updating
|
3,C |
2,B |
3,C |
| Sum of the weight to A after second
updating |
3,C |
4,B |
3,C |
| Sum of the weight to A after third updating
|
5,C |
4,B |
5,C |
| Sum of the weight to A after 4th
updating |
5,C |
6,B |
5,C |
| Sum of the weight to A after 5th
updating |
7,C |
6,B |
7,C |
| Sum of the weight to A after nth updating |
....... |
...... |
....... |
|
|
 |
 |
 |
Count to infinity problem
One way of solving this problem is that when
routers want to send information to their neighbors, don’t
send information that is related to destinations that that
neighbors are only way to link to them. For example
in this case C shouldn't give any information to B about A.
Because B is the only way to A.
|