|
A data structure that consists of a set of models and a set of
edges that relate the nodes to each other.
a graph G isG = (V,E)
where V(G) is a finite, nonempty set of vertices
E(G) is a set of edges (written as pairs of vertices)
- Vertex: A node in a graph
- Edge (arc): A pair of vertices representing a connection
between two nodes in a graph
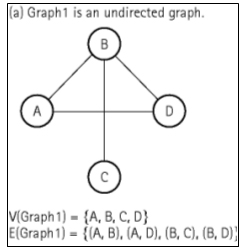
- Undirected graph: A graph in which the edges have no
direction
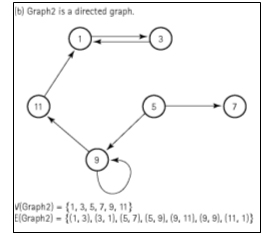
- Directed graph (digraph): A graph in which each edge
is directed from one vertex to another (or the same) vertex
- Adjacent vertices: Two vertices in a graph that are connected
by an edge
- Path: A sequence of vertices that connects two nodes
in a graph
-
loop: path that starts and edges at same vertex
-
simple path - all vertices are distinct with possible
exception of first and last being the same.
-
cycle - in a graph where the edges are directed (you
can only travel the path along the direction given), is of lenght
at least one and the starting and ending vertices are the same.\
-
acyclic - a direct graph that has no cycles (DAG - directed
acyclic graph).
- connected - an undirected graph where there is a path
from every vertex to every other vertex.
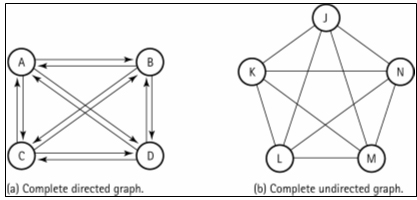
- Complete graph: A graph in which every vertex is directly
connected to every other vertex
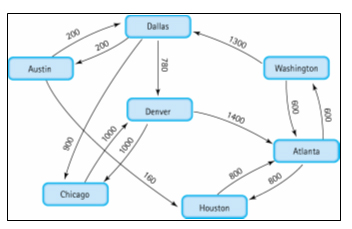
- Weighted graph: A graph in which each edge carries a
value
|
Graph ADT
Here we present ONLY the basic elements that describe a Graph
as part of our ADT.
NOTE: there are no operations to search or traverse a graph....we
will not consider this innate to the Graph ADT but, as applications
as there are many ways you could implement.
|
Variables:
- Vertices - should ideally allow for containing
different kinds of information at a vertex.
- Edges - should allow for direction if
needed as well as weight if needed.
|
|
Operations:
- Constructor : creates graph instance
- MakeEmpty: initializes graph to an empty
state
- boolean IsEmpty: tests if graph is empty
- boolean IsFull: test if graph is full
- AddVertex( VertexType vertex): Adds vertex
to graph if graph is not full.
- AddEdge( VertexType A, VertexType B, EdgeValueType
W): adds edge from A to B with weight W.
- EdgeValueTypeWeightIs(VertexType A, VertexType
B): returns weight of edge from A to B if exists.
"null-edge" if no edge exists.
- GoToVertices(VertexType A, QueType& VertexQueue):
returns a queue of vertices adjancent from vertex
A.
|
|
Other Possible Operations????
These are other possible operations that we will instead
leave as a graph applications rather than as innate operations.
- FindPath(VertexType A, VertexType B) : give
a path if one exists from vertex A to vertex B.
- FindVertex(VertexType A) : returns true
or false depending on if a Vertex is found in the graph
that matches the content in A.
- TopologicalSort(Graph g): if g is an
acyclic graph (no cylcles) than give the paths from vertices
with no incomming edges out to their "ending"
vertex.
|
|
Graph Algorithm Types
Depth-first search algorithm: Visit all the nodes in a
branch to its deepest point before moving up
Breadth-first search algorithm: Visit all the nodes on
one level before going to the next level
Single-source shortest-path algorithm: An algorithm that
displays the shortest path from a designated starting node to
every other node in the graph
|
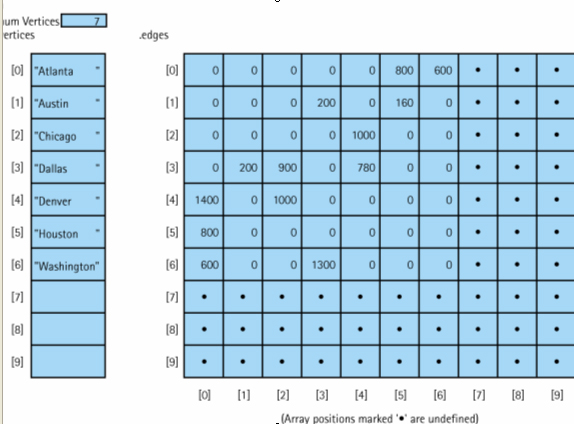
Array-Based Implementation
Adjacency Matrix: for a graph with N nodes, and N by N
table that shows the existence (and weights) of all edges in the
graph
|
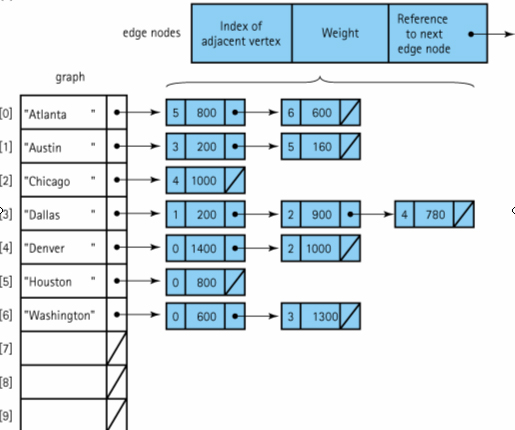
List-Based Implementation
Adjacency List: A linked list that identifies all the vertices
to which a particular vertex is connected; each vertex has its
own adjacency list
|






