CS3240: Data Structures and Algorithms |
||||||
|
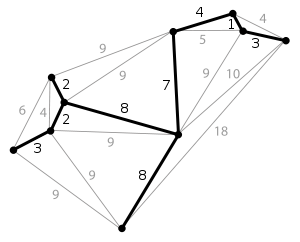
Spanning Tree
spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some (or perhaps all) of the edges of G.
forms a tree spanning every vertex.
every vertex lies in the tree, but no cycles (or loops) are formed.
Minimum Spanning Tree
a spanning tree with weight less than or equal to the weight of every other spanning tree
Application of Minimum Spanning Tree --an Example
What is the best way to run cable in a neighborhood?
If it is constrained to bury the cable only along certain paths, then there would be a graph representing which points are connected by those paths.
Some of those paths might be more expensive, because they are longer, or require the cable to be buried deeper; these paths would be represented by edges with larger weights.
A spanning tree for that graph would be a subset of those paths that has no cycles but still connects to every house. There might be several spanning trees possible. A minimum spanning tree would be one with the lowest total cost.