Depth First Search - does a path exist from vertex
A to vertex B.
Here we figure out if a path exists from A to B by searching
from A in a depth-first manner. If A and B are the same, the search
ends. Else we examine try the first of the adjacent vertices from
A and see if there is a path from it to B. If not, we try the
second one and so on until we found a path or exhausted all of
the adjacent matrices.
Example: Does a flight path exist from Austin to Washington?
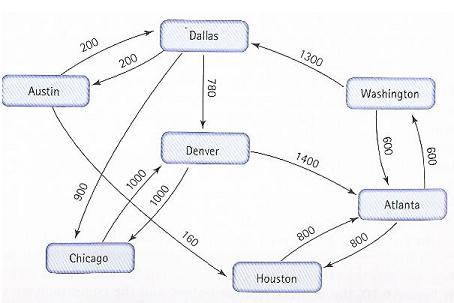
Intial PsuedoCode:
DeptFirstSearch(A, B)
{
Set found to be false
stack.Push(A) //push
on start vertex
do{
stack.Pop(vertex)
//pop of vertex on top of stack.
if
vertex = B //if
you are at the ending vertex you are done
Write
final vertex
Set
found to be true
else
Write
this vertex onto path
Push
all adjacent vertices onto stack
} while !stack.IsEmpty() AND !found
if(!found) //exhuasted
all paths and could not find path to B
Write "Path
does not exist"
}
Problem with above code:
- can cycle and revisit a vertex more than once
- could get into an infinite loop
Solution:
- mark vertices we have already visited and do not put them
on the path a second time.
- 3 new operators:
MarkVertex(VertexType vertex)
IsMarked(VertexType vertex)
- returns true/false if vertex marked or not.
ClearMarks() - sets marks
for all vertices to false.
code
Other Issues:
- What is printed out in the code presented here is the result
of the search....even the dead-ends that were found before backing
up to find the correct path. Consider the question: is there
a path from Denter to Auston. This is what are program would
print out: Denver -> Atlanta ->Houston -> Washington
-> Dallas -> Auston. But, we dont
really want to visit Houston!!!!
- This code does not necessarily find the "BEST" path.
See shortest path problem.