CS3240: Data Structures and Algorithms

Binary Search Tree Exercise

PEER GRADED

This exercise is worth 55 points

due Feb. 21 (extended to Feb. 26)

In this lab, we will work with the binary search tree. Searching for a particular item is one operation for which the binary tree is ill suited. The binary search tree is a binary tree that corrects this deficiency by organizing its data by value. Recall that each node n in a binary search tree satisfies the following three properties:

• n's value is greater than all values in its left subree T_L.
• n's value is less than all values in its right subree T_R.
• Both T_L and T_R are binary search trees.

For this exercise, you will work using an implementation of a binary search tree. You will need the following files:

• BST.h - ADT binary search tree header.
• BST.cpp - ADT binary search tree implementation.
• KeyedItem.h - KeyedItem header.
• TreeNodeBST.h - ADT binary search tree node header.
• TreeException.h - TreeException.h header.
• exercise.cpp - program that reads values from keyboard and stores them in a binary search tree.

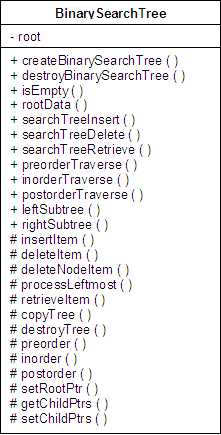
UML diagram for the class BinarySearchTree

Given the recursive nature of a binary (search) tree, a good strategy for writing a C++ function that operates on a binary (search) tree is often first to write a recursive definition of the task. Given such a recursive defition, a C++ implementation is often straightforward. Today, you will implement a set of functions involving a Binary Search Tree. You may implement each of the tasks outlined below in one function and print their results as a report, for example: (Notice that I am able to enter any kind of list - including empty to initialize my binary search tree and the entries come in any order ).

Enter a positive value (negative value to stop): 10

Enter a positive value (negative value to stop): 8

Enter a positive value (negative value to stop): 12

Enter a positive value (negative value to stop): 7

Enter a positive value (negative value to stop): 9

Enter a positive value (negative value to stop): 11

Enter a positive value (negative value to stop): 13

Enter a positive value (negative value to stop): 15

Enter a positive value (negative value to stop): -1



-------------------------------------------------

IN ORDER TRAVERSE:

7

8

9

10

11

12

13

15



a) ROOT: 10



b) NUMBER OF NODES: 8



c) SUM OF NODES: 85



d) SEARCH AND COUNT FOR VALUE: 13

   NUMBER OF COMPARISONS = 3



e) HEIGHT: 4



f) SEARCH FOR VALUES BETWEEN: 8

   AND: 12

   RESULT:

     8

     9

     10

     11

     12



g) PRINT STRUCTURED TREE:

     10

      8

       7

       9

      12

       11

       13

        15



h) INORDER TRAVERSE2:

7

8

9

10

11

12

13

15



i) INSERT NEW ITEM: 14

   NEW TREE:

     10

      8

       7

       9

      12

       11

       13

        15

         14



j) SAVE TREE IN THE FILE: out.txt



k) RESTORE TREE FROM FILE: out.txt

   NEW TREE:

     10

      8

       7

       9

      12

       11

       13

        15

         14

Note that some of these functions (a, b, c, e, f) will be added to exercise.cpp, and others (d, g, h, i, j) to the ADT files (BST.cpp, BST.h).

Tasks / To DOs

1) Implement recursive functions that perform the following tasks on arbitrary binary search trees. Add this functionalities to the file exercise.cpp:

a) Show the root value (Hint: this is straighforward without using recursivity).
b) Count the number of nodes in the tree. (Hint: If the tree is empty, the count is 0. If the tree is not empty, the count is 1 plus the number of nodes in the root's left subtree plus the number of nodes in the root's right subtree).
c) Find the sum of the elements.

2) Add the following function to the Binary search tree code (BST.h and BST.cpp):

d) int searchCount (int value): If the value is not in the tree, return 0. Otherwise, return the number of comparisons until the value is found. Then, add a function to your exercise.cpp that calls this implementation.

3) Test number 2 by creating at least 3 different trees with the same numbers, and search for one of them. For example, search for 11 in the trees: 10, 8, 12, 7, 9, 11, 13; 9, 7,12, 10, 13, 8, 11; and 7, 8, 9, 10, 11, 12, 13. Try to understand the results.

4) Add these functionalities to the file exercise.cpp:

e) Find the height of the tree.
f) Show all items that have a search key in a given range of values.

5) Add these functions to the ADT Binary search tree:

g) printTree: print a tree acppording to the following schema:

1

 2

  4

  5

 3

  6

  7

which means, 1 is the root and has two children (2 and 3), 2 has two children (4 and 5) and 3 has two children (6 and 7).
h) inorderTraverse2: iterative version (non-recursive version) of inorderTraverse using a stack as auxiliary variable.
i) insertItem2: iterative version of insertItem.
j) saveTree: save a binary search tree in a given file.
k) restoreTree: restore a binary search tree from a given file.

6)For functions in 4 &5 , implement an extra function (in exercise.cpp) that calls each one of them and print their results.

 

 

 

Deliverables

1. Show in class to peer grader
2. Take snapshots of system working and printouts - put in a document called working.doc. Must include testing all the above as illustrated above.
3. Upload code in a zipped file called code.zip to blackboard Exercise
   
   
   

Evaluation

1. This exercise will be graded by a peer (fellow student) during class. You must be present on the due date of this exercise hence to get credit on it and to participate in the grading of another student's work. (Only Valid DOCUMENTED Excuse will be allowed for missed peer grading and must be approved by instructor--evaluation process to be determined by instructor)
2. During the class session when peer grading is started, the professor will disscuss a "correct" solution with the class and you will use this and guidelines presented and discussed to grade the student's work. FOR THIS ASSIGNMENT you will demonstrate your work to your grader
3. As part of this we will explore different solutions done by students and unexpected logic errors and syntax errors.

Evaluation Guidelines

NOTE: the points on each item are given as full points if solution completely correct and 0 points if not (even if code attempted).

ITEM	Points Range
1) Add this functionalities to the file exercise.cpp: 1.a root 1.b count number of nodes 1.c sum of all elements (node values)	1.a) Show the root value (Hint: this is straighforward without using recursivity). (+5 points) 1.b) Count the number of nodes in the tree. (Hint: If the tree is empty, the count is 0. If the tree is not empty, the count is 1 plus the number of nodes in the root's left subtree plus the number of nodes in the root's right subtree). (+5 points) 1.c) Find the sum of the elements. (+5 points)
2) Add the following function to the Binary search tree code (BST.h and BST.cpp): 2.d) int searchCount (int value): If the value is not in the tree, return 0. Otherwise, return the number of comparisons until the value is found. Then, add a function to your exercise.cpp that calls this implementation.	2.d) int searchCount (int value): If the value is not in the tree, return 0. Otherwise, return the number of comparisons until the value is found. Then, add a function to your exercise.cpp that calls this implementation. (+ 5 points)
3) Test number 2 by creating at least 3 different trees with the same numbers, and search for one of them. For example, search for 11 in the trees: (10, 8, 12, 7, 9, 11, 13); (9, 7,12, 10, 13, 8, 11); and (7, 8, 9, 10, 11, 12, 13). Try to understand the results. And save the screenshot showing these results.	3) -1 point for each MISSING screenshots of searchCount(11) on each of the specified trees to the left. Screen shots must be saved in working.doc file.
4) Add these functionalities to the file exercise.cpp: e) Find the height of the tree. f) Show all items that have a search key in a given range of values.	4.e) height of tree (+5 points) 4.f) show all items that have a search key in a given range of values (+5 points)
5) Add these functions to the ADT Binary search tree: g) printTree: print a tree acppording to the following schema: 1 2 4 5 3 6 7 which means, 1 is the root and has two children (2 and 3), 2 has two children (4 and 5) and 3 has two children (6 and 7). h) inorderTraverse2: iterative version (non-recursive version) of inorderTraverse using a stack as auxiliary variable. i) insertItem2: iterative version of insertItem. j) saveTree: save a binary search tree in a given file. k) restoreTree: restore a binary search tree from a given file.	5.g)printTree function of Binary search tree class (+5 points) 5.h) inorderTraverse2: (+5 points) 5.i) insertItem2: (+5 points) 5.j) saveTree: (+5 points) 5.k) restoreTree: (+5 points)
6)For functions in 4 &5 , implement an extra function (in exercise.cpp) that calls each one of them and print their results.	6) -1 point for each MISSING screen shots of 4.e,4.f, 5.g,5.h, 5.i, 5.j, 5.k in working.doc